第132页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 某跳远队准备从甲、乙、丙、丁4名运动员中选取1名成绩优异且发挥稳定的运动员参加比赛,他们成绩的平均数和方差如下:$\overline {x}_{甲}= \overline {x}_{丁}= 5.75,\overline {x}_{乙}= \overline {x}_{丙}= 6.15,s_{甲}^{2}= s_{丙}^{2}= 0.02,s_{乙}^{2}= s_{丁}^{2}= 0.45$,则应选择的运动员是(
A. 甲
B. 乙
C. 丙
D. 丁
C
)A. 甲
B. 乙
C. 丙
D. 丁
答案:
C
2. 母题·教材P150素材 射击运动队进行射击测试,甲、乙两名选手的测试成绩如图,其成绩的方差分别记为$s_{甲}^{2}和s_{乙}^{2}$,则$s_{甲}^{2}和s_{乙}^{2}$的大小关系是(
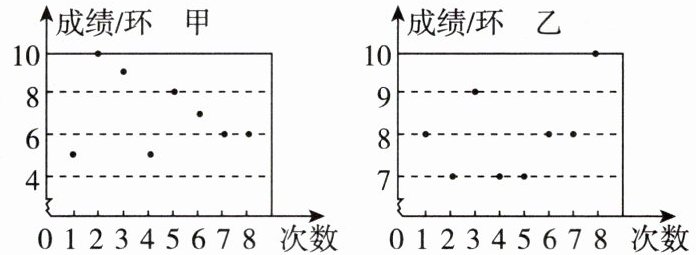
A. $s_{甲}^{2}>s_{乙}^{2}$
B. $s_{甲}^{2}<s_{乙}^{2}$
C. $s_{甲}^{2}= s_{乙}^{2}$
D. 无法确定
A
)
A. $s_{甲}^{2}>s_{乙}^{2}$
B. $s_{甲}^{2}<s_{乙}^{2}$
C. $s_{甲}^{2}= s_{乙}^{2}$
D. 无法确定
答案:
A
3. 已知一组数据33,47,47,4▲,52,56,其中一个两位数的个位数字被墨水涂污,则关于这组数据,下列统计量的计算结果与被涂污数字无关的是(
A. 平均数
B. 离差平方和
C. 众数
D. 方差
C
)A. 平均数
B. 离差平方和
C. 众数
D. 方差
答案:
C
4. 某小组五位同学参加某次考试(满分20分)的平均成绩是16分,其中三位男生成绩的方差为6,两位女生的成绩分别为17分、15分,则这五位同学成绩的标准差为(
A. $\sqrt {3}$分
B. 2分
C. $\sqrt {6}$分
D. 6分
2
)A. $\sqrt {3}$分
B. 2分
C. $\sqrt {6}$分
D. 6分
答案:
B 【点拨】设三位男生的成绩分别为a分,b分,c分.因为两位女生的成绩分别为17分、15分,所以两位女生成绩的平均数是$(17+15)÷2=16$(分),所以三位男生成绩的平均数是16分.因为三位男生成绩的方差$=\frac {1}{3}×$$[(a-16)^{2}+(b-16)^{2}+(c-16)^{2}]=6$,所以$(a-16)^{2}+$$(b-16)^{2}+(c-16)^{2}=18$,所以这个学习小组五位同学成绩的方差$=\frac {1}{5}×[(a-16)^{2}+(b-16)^{2}+(c-16)^{2}+$$(17-16)^{2}+(15-16)^{2}]=\frac {1}{5}×(18+1+1)=4$,所以标准差是$\sqrt {4}=2$(分).
5. 已知一个样本$-1,0,2,x,3$,平均数为2,则这个样本的离差平方和是
30
,方差是6
,标准差是$\sqrt {6}$
.
答案:
30;6;$\sqrt {6}$【点拨】根据题意得$(-1+0+2+x+3)÷5=$$2$,所以$x=6$.所以离差平方和是$(-1-2)^{2}+(0-2)^{2}+$$(2-2)^{2}+(6-2)^{2}+(3-2)^{2}=30$,所以方差是$30÷5=$$6$,所以标准差是$\sqrt {6}$.
6. 甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180.
(1)将下表填完整:
 (从左到右依次为
(从左到右依次为
(2)甲队队员身高的平均数为____
(3)你认为哪支仪仗队身高更为整齐?请从方差的角度说明理由.
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180.
(1)将下表填完整:
 (从左到右依次为
(从左到右依次为3
;4
;2
)(2)甲队队员身高的平均数为____
178
____厘米,乙队队员身高的平均数为____178
____厘米.(3)你认为哪支仪仗队身高更为整齐?请从方差的角度说明理由.
$s^{2}_{甲}=\frac {1}{10}[3×(177-178)^{2}+4×(178-178)^{2}+3×(179-178)^{2}]=0.6$,$s^{2}_{乙}=\frac {1}{10}[2×(176-178)^{2}+(177-178)^{2}+4×(178-178)^{2}+(179-178)^{2}+2×(180-178)^{2}]=1.8$,因为$s^{2}_{甲}<s^{2}_{乙}$,所以甲仪仗队身高更为整齐.
答案:
【解】
(1)3;4;2
(2)178;178
(3)$s^{2}_{甲}=\frac {1}{10}[3×(177-178)^{2}+4×(178-178)^{2}+3×$$(179-178)^{2}]=0.6$,
$s^{2}_{乙}=\frac {1}{10}[2×(176-178)^{2}+(177-178)^{2}+4×(178-$$178)^{2}+(179-178)^{2}+2×(180-178)^{2}]=1.8$.
因为$s^{2}_{甲}<s^{2}_{乙}$,
所以甲仪仗队身高更为整齐.
(1)3;4;2
(2)178;178
(3)$s^{2}_{甲}=\frac {1}{10}[3×(177-178)^{2}+4×(178-178)^{2}+3×$$(179-178)^{2}]=0.6$,
$s^{2}_{乙}=\frac {1}{10}[2×(176-178)^{2}+(177-178)^{2}+4×(178-$$178)^{2}+(179-178)^{2}+2×(180-178)^{2}]=1.8$.
因为$s^{2}_{甲}<s^{2}_{乙}$,
所以甲仪仗队身高更为整齐.
7. [2025邢台期中]在田径运动会“100米短跑”比赛后,嘉嘉帮助老师将20个运动员的成绩录入电脑,得到平均成绩为13.8秒,方差为3.64.后来老师核查时发现其中有2个成绩录入有误,一个错录为9秒,实际成绩是12秒;另一个错录为17秒,实际成绩是14秒,并且还漏掉了一个运动员的成绩(即嘉嘉实际按19个运动员的成绩计算),且漏掉的运动员的成绩和算错的平均成绩一样,老师将错录的2个成绩进行了更正,并加上了漏掉的运动员的成绩,更正后实际成绩的方差是$s^{2}$,则(
A. $s^{2}= 3.64$
B. $s^{2}<3.64$
C. $s^{2}>3.64$
D. 无法判断
B
)A. $s^{2}= 3.64$
B. $s^{2}<3.64$
C. $s^{2}>3.64$
D. 无法判断
答案:
B 【点拨】由题意可知,录入有误的两个数的和为$9+$$17=26$,实际的两个数的和为$12+14=26$,所以更正后实际成绩的平均数与原来的平均数相同,为13.8秒.因为$|9-13.8|>|12-13.8|,|17-13.8|>|14-13.8|$,所以方差变小,即$s^{2}<3.64$.
查看更多完整答案,请扫码查看


