《2025年综合应用创新题典中点八年级数学上册北师大版》

8. 如图,搬运师傅将滑轮固定在高为AB的楼顶上.师傅在楼底水平面上距离楼房9米的C处拉紧绳子(绳长AC),并标记,然后沿BC方向向前走7米到D处,拉紧绳子(绳长AD),量得绳长AD比绳长AC长5米,求楼的高度AB.

【解】设$AC = x$米，则$AD = (x + 5)$米。在$Rt\triangle ABC$中，$AB^{2} = AC^{2} - BC^{2} = x^{2} - 9^{2}$，在$Rt\triangle ABD$中，$AB^{2} = AD^{2} - BD^{2} = (x + 5)^{2} - (9 + 7)^{2}$，所以$x^{2} - 9^{2} = (x + 5)^{2} - (9 + 7)^{2}$，解得$x = 15$。所以$AB^{2} = 15^{2} - 9^{2} = 144$。所以楼的高度$AB$为12米。

答案： 【解】设$AC = x$米，则$AD = (x + 5)$米。在$Rt\triangle ABC$中，$AB^{2} = AC^{2} - BC^{2} = x^{2} - 9^{2}$，在$Rt\triangle ABD$中，$AB^{2} = AD^{2} - BD^{2} = (x + 5)^{2} - (9 + 7)^{2}$，所以$x^{2} - 9^{2} = (x + 5)^{2} - (9 + 7)^{2}$，解得$x = 15$。所以$AB^{2} = 15^{2} - 9^{2} = 144$。所以楼的高度$AB$为12米。

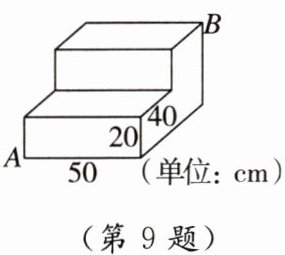
9. 如图,这是一个台阶的示意图,每一层台阶的高是20 cm、长是50 cm、宽是40 cm,一只蚂蚁沿台阶从点A出发爬到点B,其爬行的最短线路的长度是130cm.

答案： 130

10. [2025泰州期中]如图,已知三角形纸片ABC,$∠BAC= 90^{\circ }$,$AB= 2$,$AC= 3$,沿过点A的直线将纸片折叠,使点B落在边BC上的点D处；再折叠纸片,使点C与点D重合,折痕与AC的交点为E,则AE的长是______$\frac{13}{6}$.

答案： $\frac{13}{6}$【点拨】由折叠的性质可得$AD = AB = 2$，$CE = DE$，$\angle ADB = \angle B$，$\angle CDE = \angle C$。因为$\angle BAC = 90^{\circ}$，所以$\angle B + \angle C = 90^{\circ}$，所以$\angle ADB + \angle CDE = 90^{\circ}$，所以$\angle ADE = 180^{\circ} - (\angle ADB + \angle CDE) = 90^{\circ}$。设$AE = x$，则$DE = CE = AC - AE = 3 - x$。在$Rt\triangle ADE$中，由勾股定理得$AD^{2} + DE^{2} = AE^{2}$，即$2^{2} + (3 - x)^{2} = x^{2}$，解得$x = \frac{13}{6}$，所以$AE = \frac{13}{6}$。

11. 我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”.如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形的面积为25,每个直角三角形两直角边的和为7,求中间小正方形的边长.


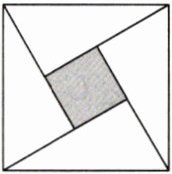
1

答案： 【解】设直角三角形的两直角边中较长边为$a$，较短边为$b$，所以大正方形的面积为$a^{2} + b^{2}$。由题意得$a^{2} + b^{2} = 25$，$a + b = 7$。因为$(a + b)^{2} = a^{2} + 2ab + b^{2}$，所以$2ab = (a + b)^{2} - (a^{2} + b^{2}) = 49 - 25 = 24$，所以$(a - b)^{2} = a^{2} + b^{2} - 2ab = 25 - 24 = 1$，所以$a - b = 1$，所以小正方形的边长为1。

12. 如图,点C为直线l上的一个动点,$AD⊥l$于点D,$BE⊥l$于点E,点E在点D右侧,并且点A,B在直线l的同侧,$AD= DE= 8$,$BE= 2$,当CD长为多少时,$\triangle ABC$为直角三角形？

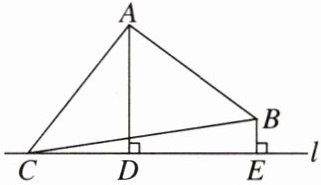
6或4或$\frac{13}{2}$

答案： 【解】过点$B$作$BF \perp AD$于点$F$，则易得四边形$DEBF$为长方形，所以$BF = DE = 8$，$DF = BE = 2$，所以$AF = AD - DF = 6$。由勾股定理得，$AB^{2} = AF^{2} + BF^{2} = 100$，$AC^{2} = 64 + CD^{2}$。当$\angle CAB = 90^{\circ}$时，点$C$在点$D$的左侧，此时$BC^{2} = (CD + 8)^{2} + 4 = CD^{2} + 16CD + 64 + 4$。由勾股定理得$AB^{2} + AC^{2} = BC^{2}$，所以$100 + 64 + CD^{2} = CD^{2} + 16CD + 64 + 4$，解得$CD = 6$；当$\angle ABC = 90^{\circ}$时，点$C$在线段$DE$上，此时$BC^{2} = (8 - CD)^{2} + 4 = CD^{2} - 16CD + 64 + 4$。由勾股定理得$AC^{2} = AB^{2} + BC^{2}$，所以$64 + CD^{2} = 100 + CD^{2} - 16CD + 64 + 4$，解得$CD = \frac{13}{2}$；当$\angle ACB = 90^{\circ}$时，易知点$C$在线段$DE$上，此时$BC^{2} = (8 - CD)^{2} + 4 = CD^{2} - 16CD + 64 + 4$。由勾股定理得$AB^{2} = AC^{2} + BC^{2}$，所以$100 = 64 + CD^{2} + CD^{2} - 16CD + 64 + 4$，所以$(CD - 4)^{2} = 0$，所以$CD = 4$。综上，当$CD$长为6或4或$\frac{13}{2}$时，$\triangle ABC$为直角三角形。