第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 下列各组数中,是勾股数的是 (
A. 6,8,10
B. 10,15,18
C. $\frac{1}{3},\frac{1}{4},\frac{1}{5}$
D. 0.3,0.4,0.5
A
)A. 6,8,10
B. 10,15,18
C. $\frac{1}{3},\frac{1}{4},\frac{1}{5}$
D. 0.3,0.4,0.5
答案:
A
2. 在$\triangle ABC$中,$\angle B= 35^{\circ}$,$BC^{2}-AC^{2}= AB^{2}$,则$\angle C$的大小为 (
A. $35^{\circ}$
B. $55^{\circ}$
C. $65^{\circ}$
D. $90^{\circ}$
B
)A. $35^{\circ}$
B. $55^{\circ}$
C. $65^{\circ}$
D. $90^{\circ}$
答案:
B
3. 母题教材P8习题T3 如图①,小霞将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处6米,如图②,则滑轮到地面的距离为 (
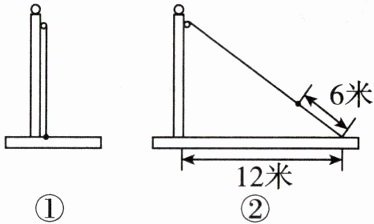
A. 9米
B. 12米
C. 15米
D. 24米
A
)
A. 9米
B. 12米
C. 15米
D. 24米
答案:
A
4. 新趋势跨学科综合 杜甫曾经哀叹“茅屋为秋风所破”,苦于杜甫不曾学过今日几何,不然也不会如此绝望.现在我们来看一茅屋的屋顶剖面(如图),它呈等腰三角形,如果屋檐$AB= AC= 5$米,横梁$BC= 8$米,那么在横梁$BC上的任意一点D处要支一根木头顶住屋顶A$处,这根木头的长度可能是 (
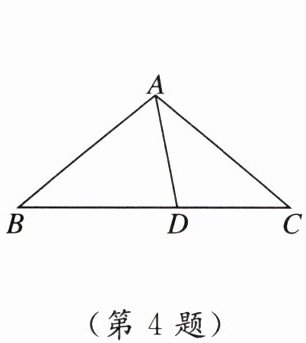
A. 2.5米
B. 6米
C. 4米
D. 8米
C
)
A. 2.5米
B. 6米
C. 4米
D. 8米
答案:
C
5. [2025郴州二模]如图所示为雷达图,规定:1个单位长度代表100m,以点$O$为原点,过数轴上的每一刻度点画同心圆,并将同心圆平均分成十二等份.一艘海洋科考船在点$O处用雷达发现A,B$两处鱼群,那么$A,B$两处鱼群的距离是 (
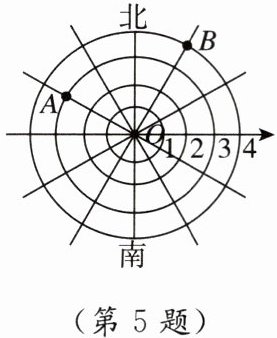
A. 5m
B. 400m
C. 500m
D. 300m
B
)
A. 5m
B. 400m
C. 500m
D. 300m
答案:
B
6. 如图,在正方形网格内,$A,B,C,D$四点都在格点上,则$\angle BAC+\angle DAC= $ (
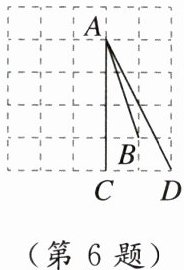
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $75^{\circ}$
B
)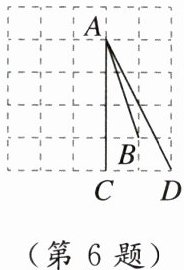
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $75^{\circ}$
答案:
B
7. 情境题生活应用 斜拉桥是我国流行的桥型之一,大跨径斜拉桥已居世界第一.如图,$OA_{1}= A_{1}A_{2}= A_{2}A_{3}= A_{3}A_{4}$,$OB_{1}= B_{1}B_{2}= B_{2}B_{3}= B_{3}B_{4}$,如果最长的钢索$A_{4}B_{4}= 80m$,那么钢索$A_{2}B_{2}$,$A_{1}B_{1}$的长分别是 (
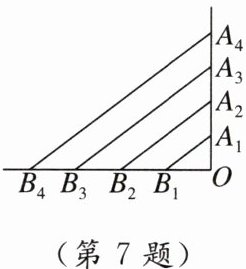
A. 60m,40m
B. 60m,30m
C. 40m,20m
D. 40m,10m
C
)
A. 60m,40m
B. 60m,30m
C. 40m,20m
D. 40m,10m
答案:
C
8. 欧几里得的《几何原本》中给出一种证明勾股定理的方法.如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,四边形$ABED$、四边形$ACGF$、四边形$BCMH和四边形AMPQ$都是正方形.若$\triangle ABC$的面积为3,正方形$ABED$的面积为13,则正方形$AMPQ$的面积为 (
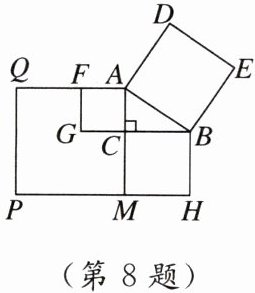
A. 16
B. 19
C. 25
D. 37
C
)
A. 16
B. 19
C. 25
D. 37
答案:
C [点拨]设BC=a,AC=b,AB=c.因为△ABC的面积为3,所以$\frac{1}{2}$ab=3,所以ab=6.因为正方形ABED的面积为13,所以AB²=c²=13.在Rt△ABC中,AB²=a²+b²=13.易知正方形AMPQ的面积为(a+b)²=a²+2ab+b²,把a²+b²=13与ab=6代入,得(a+b)²=13+2×6=25,所以正方形AMPQ的面积为25.
9. 长方体木箱的长、宽、高分别为12cm,4cm,3cm则能放进木箱中的直木棒最长为
13
cm.
答案:
13
10. 如图,某港口$P$位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12n mile和16n mile,1h后两轮船分别位于点$A,B$处,且相距20n mile.如果知道甲轮船沿北偏西$40^{\circ}$方向航行,则乙轮船沿
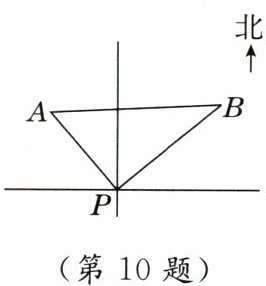
北偏东50°(或东偏北40°)
方向航行.
答案:
北偏东50°(或东偏北40°)
查看更多完整答案,请扫码查看


