第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 母题教材P103习题T10 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶路程随时间变化的图象.则下列结论错误的是(
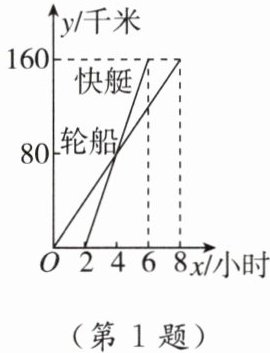
A. 轮船的速度为20千米/时
B. 快艇的速度为40千米/时
C. 轮船比快艇先出发2小时
D. 快艇到达乙港用了6小时
D
)
A. 轮船的速度为20千米/时
B. 快艇的速度为40千米/时
C. 轮船比快艇先出发2小时
D. 快艇到达乙港用了6小时
答案:
1. D
2. [2025聊城月考]小王同学从家出发,步行到离家a m的公园晨练,4 min后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:m)与出发时间x(单位:min)的函数关系如图所示,则两人先后两次相遇的时间间隔为(
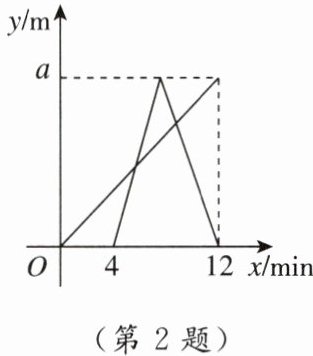
A. 2.7 min
B. 2.8 min
C. 3 min
D. 3.2 min
C
)
A. 2.7 min
B. 2.8 min
C. 3 min
D. 3.2 min
答案:
2. C [点拨]由题图可得小王的速度为$\frac{a}{12}$m/min,爸爸的速度为$\frac{a}{(12 - 4)÷2}=\frac{a}{4}$(m/min)。设小王出发$m$min两人第一次相遇,出发$n$min两人第二次相遇,则$\frac{a}{12}m=(m - 4)×\frac{a}{4}$,$\frac{a}{12}n+\frac{a}{4}[n - 4 - (12 - 4)÷2]=a$,解得$m = 6$,$n = 9$。所以$n - m = 9 - 6 = 3$。故选C。
3. [2025太原迎泽区月考]某快递公司每天下午15:00~16:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,如图,线段BC,DE分别表示甲仓库、乙仓库的快件数量$y_{1},y_{2}$(件)与揽件(或派件)时间x(分钟)之间的函数关系,线段BC,DE相交于点A.
(1)求甲仓库快件数量$y_{1}$(件)与揽件时间x(分钟)之间的函数表达式$(0≤x≤60);$
(2)若已知乙仓库快件数量$y_{2}$(件)与派件时间x(分钟)之间的函数表达式是$y_{2}= -4x+240,$
则点A的坐标为(
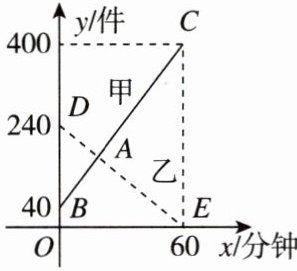
(1)求甲仓库快件数量$y_{1}$(件)与揽件时间x(分钟)之间的函数表达式$(0≤x≤60);$
(2)若已知乙仓库快件数量$y_{2}$(件)与派件时间x(分钟)之间的函数表达式是$y_{2}= -4x+240,$
则点A的坐标为(
20
,160),点A的坐标表示的实际意义是经过20分钟,甲乙两个仓库中的快件数量相等,均为160件
.
答案:
3. [解]
(1)设$y_{1}=kx+b(k≠0)$,由题图可知,$y_{1}=kx+b$的图象过点$(0,40)$,$(60,400)$,所以$b = 40$,$60k + b = 400$,解得$b = 40$,$k = 6$。所以$y_{1}=6x + 40(0≤x≤60)$。
(2)20;经过20分钟,甲乙两个仓库中的快件数量相等,均为160件
(1)设$y_{1}=kx+b(k≠0)$,由题图可知,$y_{1}=kx+b$的图象过点$(0,40)$,$(60,400)$,所以$b = 40$,$60k + b = 400$,解得$b = 40$,$k = 6$。所以$y_{1}=6x + 40(0≤x≤60)$。
(2)20;经过20分钟,甲乙两个仓库中的快件数量相等,均为160件
4. 甲、乙两个工程队分别同时挖掘两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的函数关系如图所示,以下信息一定正确的有(
①甲队挖掘20 m,用了2 h;
②开挖6 h后,甲队比乙队多挖掘10 m;
③乙队从开挖2 h后到6 h之间,每小时挖掘5 m;
④开挖4 h后,甲、乙两队所挖河渠长度相等.
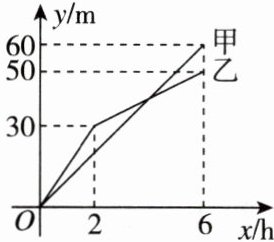
A. 1个
B. 2个
C. 3个
D. 4个
①②③④
)①甲队挖掘20 m,用了2 h;
②开挖6 h后,甲队比乙队多挖掘10 m;
③乙队从开挖2 h后到6 h之间,每小时挖掘5 m;
④开挖4 h后,甲、乙两队所挖河渠长度相等.

A. 1个
B. 2个
C. 3个
D. 4个
答案:
4. D [点拨]由题图可知,开挖6h,甲队一共挖掘60m,所以甲队的速度为$\frac{60}{6}=10$(m/h)。所以甲队挖掘20m,用了2h,故①正确;由题图可知,开挖6h后,甲队挖掘了60m,乙队挖掘了50m,则甲队比乙队多挖掘10m,故②正确;由题图可知,乙队从开挖2h后到6h之间挖了$50 - 30 = 20$(m),则每小时挖掘5m,故③正确;开挖4h后,甲队挖了$10×4 = 40$(m),乙队挖了$30 + 5×(4 - 2)=40$(m),则开挖4h后,甲、乙两队所挖河渠长度相等,故④正确。
5. 情境题方案策略型 春节临近,某网商紧急备货,但目前缺少大量礼品盒,该网商通过调研,发现这种礼品盒的来源有两种方案:
方案一:从纸箱厂订购,购买所需费用$y_{1}$(单位:元)与礼品盒的数量x(单位:盒)满足如图所示的函数关系.
方案二:从纸箱厂租赁机器,自己加工制作这种礼品盒,所需费用(包括租赁机器的费用和生产礼品盒的费用)$y_{2}$(单位:元)与礼品盒的数量x(单位:盒)满足如图所示的函数关系.
请回答下列问题:
(1)方案一中,礼品盒的单价为____
(2)请直接写出$y_{1},y_{2}$关于x的函数表达式.
$y_{1}=$
(3)如何选择方案,才能够更省钱?请说明理由.
当$x=1000$时,两种方案同样省钱;当$x<1000$时,选择方案一更省钱;当$x>1000$时,选择方案二更省钱。
方案一:从纸箱厂订购,购买所需费用$y_{1}$(单位:元)与礼品盒的数量x(单位:盒)满足如图所示的函数关系.
方案二:从纸箱厂租赁机器,自己加工制作这种礼品盒,所需费用(包括租赁机器的费用和生产礼品盒的费用)$y_{2}$(单位:元)与礼品盒的数量x(单位:盒)满足如图所示的函数关系.
请回答下列问题:
(1)方案一中,礼品盒的单价为____
3
____元.(2)请直接写出$y_{1},y_{2}$关于x的函数表达式.
$y_{1}=$
$3x$
,$y_{2}=$$2x + 1000$
。(3)如何选择方案,才能够更省钱?请说明理由.
当$x=1000$时,两种方案同样省钱;当$x<1000$时,选择方案一更省钱;当$x>1000$时,选择方案二更省钱。
答案:
5. [解]
(1)3
(2)$y_{1}=3x$,$y_{2}=2x + 1000$。[点拨]设$y_{1}$关于$x$的函数表达式为$y_{1}=k_{1}x$。因为该函数图象经过点$(500,1500)$,所以$1500 = 500k_{1}$,解得$k_{1}=3$。所以$y_{1}$关于$x$的函数表达式为$y_{1}=3x$。设$y_{2}$关于$x$的函数表达式为$y_{2}=k_{2}x + b$。因为该函数图象经过点$(0,1000)$和$(1500,4000)$,所以$1500k_{2}+b = 4000$,$b = 1000$,解得$k_{2}=2$。所以$y_{2}$关于$x$的函数表达式为$y_{2}=2x + 1000$。
(3)令$3x = 2x + 1000$,解得$x = 1000$,所以当$x = 1000$时,两种方案同样省钱;当$x<1000$时,选择方案一更省钱;当$x>1000$时,选择方案二更省钱。
(1)3
(2)$y_{1}=3x$,$y_{2}=2x + 1000$。[点拨]设$y_{1}$关于$x$的函数表达式为$y_{1}=k_{1}x$。因为该函数图象经过点$(500,1500)$,所以$1500 = 500k_{1}$,解得$k_{1}=3$。所以$y_{1}$关于$x$的函数表达式为$y_{1}=3x$。设$y_{2}$关于$x$的函数表达式为$y_{2}=k_{2}x + b$。因为该函数图象经过点$(0,1000)$和$(1500,4000)$,所以$1500k_{2}+b = 4000$,$b = 1000$,解得$k_{2}=2$。所以$y_{2}$关于$x$的函数表达式为$y_{2}=2x + 1000$。
(3)令$3x = 2x + 1000$,解得$x = 1000$,所以当$x = 1000$时,两种方案同样省钱;当$x<1000$时,选择方案一更省钱;当$x>1000$时,选择方案二更省钱。
查看更多完整答案,请扫码查看


