《2025年综合应用创新题典中点八年级数学上册北师大版》

10. 新考法方程思想 两组数据:3,x,2y,5与x,6,y的平均数都是6,若将这两组数据合并为一组新数据:3,x,2y,5,x,6,y,则这组新数据的众数为8.

答案： 8

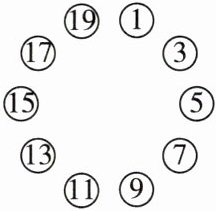
11. 情境题游戏活动型 有10个同学围成一圈做游戏,游戏规则是:每个人心里都想好一个数,并把想好的这个数如实地告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若这10个同学报出来的数如图所示,则报5的同学心里所想的数是______-5.

答案： 【点拨】设报 5 的同学心里想的数是 $x$。因为报 5 与报 9 的两个人心里想的数的平均数是 7，所以报 9 的人心里想的数应是 $14 - x$。所以报 13 的人心里想的数是 $22 - (14 - x) = 8 + x$。所以报 17 的人心里想的数是 $30 - (8 + x) = 22 - x$。所以报 1 的人心里想的数是 $38 - (22 - x) = 16 + x$。因为报 1 的人与报 5 的人心里想的数的平均数是 3，所以 $16 + x + x = 2 \times 3$，解得 $x = -5$。所以报 5 的同学心里所想的数是 -5。

12. 新考向传统文化 2024年12月4日,中国“春节”申遗成功.中国春节文化源远流长,全国各地衍生出纷繁多样的春节习俗.某校为了解学生对春节文化的了解情况,举办了春节文化知识竞赛,现从该校七、八年级学生中各随机抽取20名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分为四组:A.$90\leqslant x\leqslant 100$,B.$80\leqslant x\lt 90$,C.$70\leqslant x\lt 80$,D.$x\lt 70$,得分在90分及以上为优秀),下面给出了部分信息:
七年级20名学生的竞赛成绩是:
64,68,72,80,83,85,86,88,89,89,
90,93,93,93,95,96,98,99,99,100.
八年级20名学生竞赛成绩在B组的数据是83,85,86,87,88,89,89.
七、八年级抽取的学生 八年级抽取的学生竞赛成绩统计表
根据以上信息,解答下列问题:
(1)上述图表中的$a = $88,$b = $93,$m = $35.
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的春节文化知识竞赛成绩更好?请说明理由.
(3)若该校七年级有700名,八年级有800名学生参加了此次春节文化知识竞赛,估计该校七、八年级学生参加此次春节文化知识竞赛成绩达到优秀的共有多少人?

答案： 【解】
(1)88；93；35
(2)（答案不唯一）我认为八年级学生的春节文化知识竞赛成绩更好，因为八年级学生与七年级学生竞赛成绩的平均数相等，八年级学生竞赛成绩的众数比七年级学生竞赛成绩的众数高，所以八年级学生的春节文化知识竞赛成绩更好。
(3)估计该校七、八年级学生参加此次春节文化知识竞赛成绩达到优秀的共有 $700 × \frac{10}{20} + 800 × 40\% = 670$（人）。

13. 新趋势学科内综合 已知有理数-9,7,14在数轴上对应的点分别为A,B,C.
(1)若数轴上点D表示的数为$\frac{-9 + 7 + 14}{3}$,求线段AD的长;
(2)再添加一个数a,数轴上点E表示的数为-9,7,14和a四个数的平均数,若线段$DE = 1$,求a的值.

答案： 【解】
(1)因为 $\frac{-9 + 7 + 14}{3} = 4$，
所以点 $D$ 表示的数为 4。
因为点 $A$ 表示的数为 -9，
所以 $AD = 4 - (-9) = 13$。
(2)因为 $DE = 1$，点 $D$ 表示的数为 4，
所以点 $E$ 表示的数为 $4 + 1 = 5$ 或 $4 - 1 = 3$。
因为点 $E$ 表示的数为 -9，7，14 和 $a$ 四个数的平均数，
所以 $5 \times 4 = -9 + 7 + 14 + a$ 或 $3 \times 4 = -9 + 7 + 14 + a$。
所以 $a = 8$ 或 $a = 0$。