第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
11. [2024河北]已知a,b,n均为正整数.
(1)若$n<\sqrt {10}<n+1$,则$n=$
(2)若$n-1<\sqrt {a}<n,n<\sqrt {b}<n+1$,则满足条件的a的个数总比b的个数少
(1)若$n<\sqrt {10}<n+1$,则$n=$
3
;(2)若$n-1<\sqrt {a}<n,n<\sqrt {b}<n+1$,则满足条件的a的个数总比b的个数少
2
个.
答案:
(1)3
(2)2 【点拨】
(1)因为$\sqrt{9}<\sqrt{10}<\sqrt{16}$,所以$3<\sqrt{10}<4$.因为$n<\sqrt{10}<n+1$,n为正整数,所以$n=3$.
(2)因为$n - 1<\sqrt{a}<n$,所以$(n - 1)^{2}<a<n^{2}$,所以a的取值范围为$n^{2}-(n - 1)^{2}=n^{2}-n^{2}+2n - 1=2n - 1$.因为$n<\sqrt{b}<n + 1$,所以$n^{2}<b<(n + 1)^{2}$,所以b的取值范围为$(n + 1)^{2}-n^{2}=n^{2}+2n + 1 - n^{2}=2n + 1$.因为$(2n + 1)-(2n - 1)=2$,所以满足条件的a的个数总比b的个数少2个.
(1)3
(2)2 【点拨】
(1)因为$\sqrt{9}<\sqrt{10}<\sqrt{16}$,所以$3<\sqrt{10}<4$.因为$n<\sqrt{10}<n+1$,n为正整数,所以$n=3$.
(2)因为$n - 1<\sqrt{a}<n$,所以$(n - 1)^{2}<a<n^{2}$,所以a的取值范围为$n^{2}-(n - 1)^{2}=n^{2}-n^{2}+2n - 1=2n - 1$.因为$n<\sqrt{b}<n + 1$,所以$n^{2}<b<(n + 1)^{2}$,所以b的取值范围为$(n + 1)^{2}-n^{2}=n^{2}+2n + 1 - n^{2}=2n + 1$.因为$(2n + 1)-(2n - 1)=2$,所以满足条件的a的个数总比b的个数少2个.
12. 某地气象资料表明:当地雷雨持续的时间t(单位:h)可以用公式$t^{2}= \frac {d^{3}}{900}$来估计,其中d(单位:km)是雷雨区域的直径.
(1)如果某场雷雨区域的直径是10 km,那么这场雷雨大约能持续多长时间? (结果保留根号)
(2)如果这场雷雨持续了20 min,那么这场雷雨区域的直径大约是多少? (结果精确到0.1 km)
(1)如果某场雷雨区域的直径是10 km,那么这场雷雨大约能持续多长时间? (结果保留根号)
(2)如果这场雷雨持续了20 min,那么这场雷雨区域的直径大约是多少? (结果精确到0.1 km)
答案:
【解】
(1)把$d = 10$代入$t^{2}=\frac{d^{3}}{900}$,得$t^{2}=\frac{10^{3}}{900}=\frac{1000}{900}$.所以$t=\sqrt{\frac{1000}{900}}=\frac{\sqrt{10}}{3}$.所以这场雷雨大约能持续$\frac{\sqrt{10}}{3}h$.
(2)$20min=\frac{1}{3}h$.把$t=\frac{1}{3}$代入$t^{2}=\frac{d^{3}}{900}$,得$(\frac{1}{3})^{2}=\frac{d^{3}}{900}$.所以$d=\sqrt[3]{100}\approx4.6$.所以这场雷雨区域的直径大约是4.6km.
(1)把$d = 10$代入$t^{2}=\frac{d^{3}}{900}$,得$t^{2}=\frac{10^{3}}{900}=\frac{1000}{900}$.所以$t=\sqrt{\frac{1000}{900}}=\frac{\sqrt{10}}{3}$.所以这场雷雨大约能持续$\frac{\sqrt{10}}{3}h$.
(2)$20min=\frac{1}{3}h$.把$t=\frac{1}{3}$代入$t^{2}=\frac{d^{3}}{900}$,得$(\frac{1}{3})^{2}=\frac{d^{3}}{900}$.所以$d=\sqrt[3]{100}\approx4.6$.所以这场雷雨区域的直径大约是4.6km.
13. 某数学兴趣小组准备探究无理数.
(1)$\sqrt {2}$到底有多大? 下面是探索$\sqrt {2}$的近似值的过程,请补充完整;
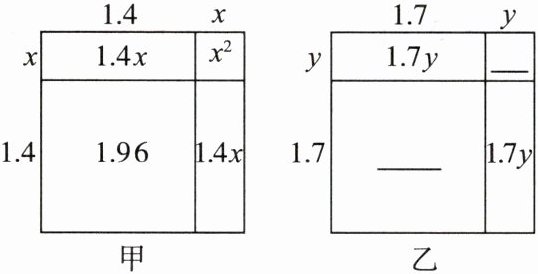
如图甲所示,我们知道面积是2的正方形边长是$\sqrt {2}$,且$\sqrt {2}>1.4$.设$\sqrt {2}= 1.4+x.$
由图甲可得,$x^{2}+2.8x+1.96= 2.$
因为x值很小,所以$x^{2}$更小,略去$x^{2}$,得方程$2.8x+1.96= 2,$
解得$x\approx $____(保留到0.001),
即$\sqrt {2}\approx $____;
(2)数学兴趣小组依据上面的方法接着探究$\sqrt {3}$的近似值,如图乙所示,面积是3的正方形边长是$\sqrt {3}$,且$\sqrt {3}>1.7$.设$\sqrt {3}= 1.7+y,... $,请把图乙和剩余的过程补充完整(结果保留到0.001);
(3)怎样画出$\sqrt {2}和\sqrt {5}$,请一起参与探索画的过程.
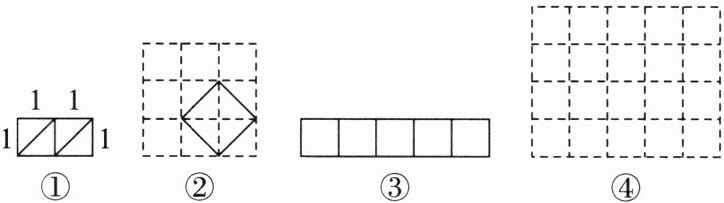
该兴趣小组的做法是:设新正方形的边长为$x(x>0)$.依题意,割补前后图形的面积相等,有$x^{2}= 2$,解得$x= \sqrt {2}$.把2个边长为1的正方形,如图①所示进行分割,然后在图②中用实线画出拼接成的新正方形.如图③所示,现有5个边长为1的正方形,请参考上面的做法,把它们分割后拼接成一个新的正方形.要求:在图③中画出分割线,并在图④中用实线画出拼接成的新正方形,直接画出图形即可.
(1)$\sqrt {2}$到底有多大? 下面是探索$\sqrt {2}$的近似值的过程,请补充完整;
如图甲所示,我们知道面积是2的正方形边长是$\sqrt {2}$,且$\sqrt {2}>1.4$.设$\sqrt {2}= 1.4+x.$
由图甲可得,$x^{2}+2.8x+1.96= 2.$

因为x值很小,所以$x^{2}$更小,略去$x^{2}$,得方程$2.8x+1.96= 2,$
解得$x\approx $____(保留到0.001),
即$\sqrt {2}\approx $____;
(2)数学兴趣小组依据上面的方法接着探究$\sqrt {3}$的近似值,如图乙所示,面积是3的正方形边长是$\sqrt {3}$,且$\sqrt {3}>1.7$.设$\sqrt {3}= 1.7+y,... $,请把图乙和剩余的过程补充完整(结果保留到0.001);
(3)怎样画出$\sqrt {2}和\sqrt {5}$,请一起参与探索画的过程.
该兴趣小组的做法是:设新正方形的边长为$x(x>0)$.依题意,割补前后图形的面积相等,有$x^{2}= 2$,解得$x= \sqrt {2}$.把2个边长为1的正方形,如图①所示进行分割,然后在图②中用实线画出拼接成的新正方形.如图③所示,现有5个边长为1的正方形,请参考上面的做法,把它们分割后拼接成一个新的正方形.要求:在图③中画出分割线,并在图④中用实线画出拼接成的新正方形,直接画出图形即可.

答案:
【解】
(1)0.014;1.414
(2)2.89;$y^{2}$由题图乙可得,$y^{2}+3.4y+2.89=3$.因为y值很小,所以$y^{2}$更小,略去$y^{2}$,得方程$3.4y+2.89=3$,解得$y\approx0.032$,即$\sqrt{3}\approx1.732$.
(3)如图①②所示.

【解】
(1)0.014;1.414
(2)2.89;$y^{2}$由题图乙可得,$y^{2}+3.4y+2.89=3$.因为y值很小,所以$y^{2}$更小,略去$y^{2}$,得方程$3.4y+2.89=3$,解得$y\approx0.032$,即$\sqrt{3}\approx1.732$.
(3)如图①②所示.

查看更多完整答案,请扫码查看


