《2025年综合应用创新题典中点八年级数学上册北师大版》

15. 已知$\sqrt{1 - 3b}与\sqrt{2a + 1}$互为相反数,求$-3b + 2a + 6$的平方根.

答案： 【解】由题意得$\sqrt{1-3b}+\sqrt{2a+1}=0$。
因为$\sqrt{1-3b} \geq 0$，$\sqrt{2a+1} \geq 0$，
所以$1-3b=0$，$2a+1=0$，
解得$a=-\frac{1}{2}$，$b=\frac{1}{3}$，
所以$-3b+2a+6=-3 \times \frac{1}{3}+2 \times (-\frac{1}{2})+6=4$，
所以其平方根为$\pm 2$。

16. 立德树人保护环境 “保护环境,节约资源”一直是现代社会所提倡的,墨墨参加了学校组织的“节约资源,废物利用”比赛,他想将一个废旧易拉罐的侧面制成一个正方体(有底有盖)储存盒,他测得该废旧易拉罐的高是20cm,底面直径是10cm,废旧易拉罐的侧面刚好用完,正方体储存盒的接头部分忽略不计,求墨墨所做的正方体储存盒的棱长.($\pi$取3)

答案： 【解】设墨墨所做的正方体储存盒的棱长为$x$cm。
由题意，得$6x^{2}=20 \times 3 \times 10$，
解得$x=10$（负值已舍去）。
答：墨墨所做的正方体储存盒的棱长为10cm。

17. 新考法归纳法 归纳与探究：
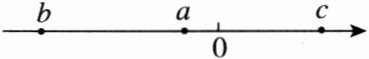
(1)计算：$\sqrt{2^{2}}=$2,$\sqrt{(\frac{2}{3})^{2}}=$$\frac{2}{3}$,$\sqrt{(-3)^{2}}=$3,$\sqrt{(-\frac{1}{4})^{2}}=$$\frac{1}{4}$,$\sqrt{0^{2}}=$0,…
(2)猜想：对于任意有理数$a$,$\sqrt{a^{2}}$一定等于$a$吗？利用(1)中的计算,你发现$\sqrt{a^{2}}$的值等于多少呢？
对于任意有理数$a$，$\sqrt{a^{2}}$不一定等于$a$。由(1)中各式的计算结果可以发现：对于任意有理数$a$，有$\sqrt{a^{2}}=\begin{cases}a(a \geq 0) \\ -a(a ＜ 0)\end{cases}$。
(3)应用：有理数$a,b,c$在数轴上所对应的点如图所示,$c$是4的平方根.计算：$|b - a|-\sqrt{b^{2}}+\sqrt{(c - a)^{2}}$.
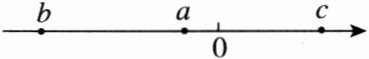
由数轴可知$b-a ＜ 0$，$b ＜ 0$，$c-a ＞ 0$，$c ＞ 0$，所以原式$=a-b-(-b)+(c-a)=a-b+b+c-a=c$。因为$c$是4的平方根，且$c ＞ 0$，所以$c=2$，所以原式$=2$。

答案： 【解】
(1)2；$\frac{2}{3}$；3；$\frac{1}{4}$；0
(2)对于任意有理数$a$，$\sqrt{a^{2}}$不一定等于$a$。由
(1)中各式的计算结果可以发现：对于任意有理数$a$，有$\sqrt{a^{2}}=\begin{cases}a(a \geq 0) \\ -a(a ＜ 0)\end{cases}$。
(3)由数轴可知$b-a ＜ 0$，$b ＜ 0$，$c-a ＞ 0$，$c ＞ 0$，
所以原式$=a-b-(-b)+(c-a)=a-b+b+c-a=c$。
因为$c$是4的平方根，且$c ＞ 0$，所以$c=2$，所以原式$=2$。

18. 新考法·分类讨论法 喜欢探索数学知识的小明遇到一个新的定义：对于三个正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个数为“和谐组合”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”,例：1,4,9这三个数,$\sqrt{1×4}= 2,\sqrt{1×9}= 3,\sqrt{4×9}= 6$,其结果分别为2,3,6,都是整数,所以1,4,9三个数称为“和谐组合”,其中“最小算术平方根”是2,“最大算术平方根”是6.
(1)3,12,16____不是“和谐组合”.(填“是”或“不是”)
(2)请说明2,8,18这三个数是“和谐组合”,并求出“最小算术平方根”和“最大算术平方根”；
(3)已知4,$a$,25三个数是“和谐组合”,且“最大算术平方根”是“最小算术平方根”的5倍,求$a$的值.1或100

答案： 【解】
(1)不是
(2)因为$\sqrt{2 \times 18}=6$，$\sqrt{2 \times 8}=4$，$\sqrt{18 \times 8}=12$，且6，4，12都是整数，所以2，8，18这三个数是“和谐组合”，其中“最小算术平方根”是4，“最大算术平方根”是12。
(3)分三种情况：①当$4 \leq a \leq 25$时，$\sqrt{25a}=5\sqrt{4a}$，解得$a=0$（舍去）；
②当$a ＜ 4$时，$\sqrt{4 \times 25}=5\sqrt{4a}$，解得$a=1$；
③当$a ＞ 25$时，$\sqrt{25a}=5\sqrt{4 \times 25}$，解得$a=100$。
综上所述，$a$的值为1或100。