《2025年综合应用创新题典中点八年级数学上册北师大版》

1. 下列各式是二次根式的是(B)
A. $\sqrt { - 4 }$
B. $\sqrt { 5 }$
C. $\sqrt { 2 - \pi }$
D. $\sqrt [ 3 ] { 8 }$

答案： B

2. 如果$\sqrt { x - 1 } + \sqrt { 9 - x }$有意义,那么代数式$| x - 1 | + \sqrt { ( x - 9 ) ^ { 2 } }$的值为(B)
A. $\pm 8$
B. 8
C. $- 8$
D. 无法确定

答案： B

3. 下列二次根式中,是最简二次根式的是(B)
A. $\sqrt { 25 a }$
B. $\sqrt { a ^ { 2 } + b ^ { 2 } }$
C. $\sqrt { \frac { a } { 2 } }$
D. $\sqrt { 0.5 }$

答案： B

4. 小明的作业本上有以下四题:①$\sqrt { 16 a ^ { 4 } } = 4 a ^ { 2 }$;②$\sqrt { 5 a } \cdot \sqrt { 10 a } = 5 \sqrt { 2 } a$;③$a \sqrt { \frac { 1 } { a } } = \sqrt { a ^ { 2 } \cdot \frac { 1 } { a } } = \sqrt { a }$;④$\sqrt { 8 a } ÷ \sqrt { 2 a } = 4$. 做错的题是(D)
A. ①
B. ②
C. ③
D. ④

答案： D

5. 如果最简二次根式$\sqrt [ b - a ] { 3 b }$和$\sqrt { 2 b - a + 2 }$可以合并,那么$a$,$b$的值为(D)
A. $a = 1$,$b = - 2$
B. $a = - 1$,$b = 1$
C. $a = 2$,$b = 0$
D. $a = 0$,$b = 2$

答案： D

6. $\sqrt { 10 }的整数部分是x$,小数部分是$y$,则$y ( x + \sqrt { 10 } )$的值是(A)
A. 1
B. 2
C. 3
D. 4

答案： A

7. 新视角 规律探究题 小明做数学题时,发现$\sqrt { 1 - \frac { 1 } { 2 } } = \sqrt { \frac { 1 } { 2 } }$;$\sqrt { 2 - \frac { 2 } { 5 } } = 2 \sqrt { \frac { 2 } { 5 } }$;$\sqrt { 3 - \frac { 3 } { 10 } } = 3 \sqrt { \frac { 3 } { 10 } }$;$\sqrt { 4 - \frac { 4 } { 17 } } = 4 \sqrt { \frac { 4 } { 17 } }$;…$$. 按此规律,若$\sqrt { a - \frac { 8 } { b } } = a \sqrt { \frac { 8 } { b } }$($a$,$b$为正整数),则$a + b = $(D)
A. 64
B. 72
C. 65
D. 73

答案： D

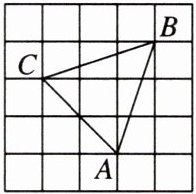
8. 如图,方格纸中小正方形的边长为1,$\triangle A B C$的三个顶点都在小正方形的格点上,某同学在观察探究时发现:①$\triangle A B C$的形状是等腰三角形;②$\triangle A B C的周长是2 \sqrt { 10 } + \sqrt { 2 }$;③点$C到A B边的距离是\frac { 4 } { 5 } \sqrt { 10 }$. 你认为该同学观察的结论正确的序号是(①③)

A. ①②
B. ①③
C. ②③
D. ①②③

答案： B 【点拨】因为方格纸中小正方形的边长为 1，$\triangle ABC$的三个顶点都在小正方形的格点上，所以$AB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$，$BC=\sqrt{1^{2}+3^{2}}=\sqrt{10}$。所以$AB=BC$。所以$\triangle ABC$是等腰三角形，故①的结论正确；因为$AC=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$，所以$\triangle ABC$的周长为$AB + BC + AC=\sqrt{10}+\sqrt{10}+2\sqrt{2}=2\sqrt{10}+2\sqrt{2}$，故②的结论错误；因为$S_{\triangle ABC}=3^{2}-\frac{1}{2}\times1\times3-\frac{1}{2}\times2\times2-\frac{1}{2}\times1\times3=9-\frac{3}{2}-2-\frac{3}{2}=4$，所以点$C$到$AB$边的距离为$2\times4\div\sqrt{10}=\frac{4}{5}\sqrt{10}$，故③的结论正确。

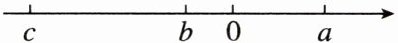
9. 新考法 数形结合法 实数$a$,$b$,$c$在数轴上的对应点如图所示,化简$\sqrt { ( a - c ) ^ { 2 } } - | b - a |$的结果是$b - c$.

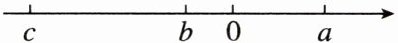
答案： $b - c$

10. 新考向 数学文化 古希腊几何学家海伦和我国南宋数学家秦九韶曾提出利用三角形的三边求面积的公式,称为海伦—秦九韶公式. 如果一个三角形的三边长分别是$a$,$b$,$c$,记$p = \frac { a + b + c } { 2 }$,那么这个三角形的面积为$S = \sqrt { p ( p - a ) ( p - b ) ( p - c ) }$. 若$a = 5$,$b = 8$,$c = 7$,其面积$S的整数部分为m$,则$m$的值为17.

答案： 17

11. 新考法 整体代入法 已知$x - y = \sqrt { 3 }$,求代数式$( x + 1 ) ^ { 2 } - 2 x + y ( y - 2 x )$的值为____4.

答案： 4

12. 新视角 新定义题 对于任意两个和为正数的实数$a$,$b$,定义运算“※”如下:$a ※ b = \frac { a - b } { \sqrt { a + b } }$,例如$3 ※ 1 = \frac { 3 - 1 } { \sqrt { 3 + 1 } } = 1$. 那么$8 ※ 12 = $$-\frac{2\sqrt{5}}{5}$.

答案： $-\frac{2\sqrt{5}}{5}$