《2025年综合应用创新题典中点八年级数学上册北师大版》

12. 新考法 阅读类比法 阅读一段文字,再回答下列问题：已知在平面内两点的坐标为$P_{1}(x_{1},y_{1})$,$P_{2}(x_{2},y_{2})$,则该两点间距离公式为$P_{1}P_{2}= \sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$,同时,当两点在同一坐标轴上或所在直线平行于$x轴或平行于y$轴时,两点间的距离公式可化简成$|x_{1}-x_{2}|或|y_{1}-y_{2}|$。
(1)若已知两点$A(3,3)$,$B(-2,-1)$,则$A$,$B$两点间的距离为√41；
(2)已知点$M$,$N在平行于y$轴的直线上,点$M的纵坐标为7$,点$N的纵坐标为-2$,则$M$,$N$两点间的距离为9；
(3)已知一个三角形各顶点的坐标为$A(-1,\frac {1}{2})$,$B(-\frac {5}{3},\frac {5}{6})$,$C(\frac {1}{3},\frac {19}{6})$,请求出该图形的面积。10/9

答案： [解]
(1)√41
(2)9 [点拨]因为点M，N在平行于y轴的直线上，点M的纵坐标为7，点N的纵坐标为−2，所以MN = |−2 - 7| = 9。即M，N两点间的距离是9。
(3)因为一个三角形各顶点的坐标为A(−1,1/2)，B(−5/3,5/6)，C(1/3,19/6)，
所以AB = √((−1 + 5/3)² + (1/2 - 5/6)²) = √5/3，
AC = √((−1 - 1/3)² + (1/2 - 19/6)²) = 4√5/3，
BC = √((−5/3 - 1/3)² + (5/6 - 19/6)²) = √85/3。
所以AB² + AC² = (√5/3)² + (4√5/3)² = 85/9 = BC²，
所以△ABC是直角三角形，且∠ABC = 90°。
所以S△ABC = 1/2AB·AC = 1/2×√5/3×4√5/3 = 10/9。

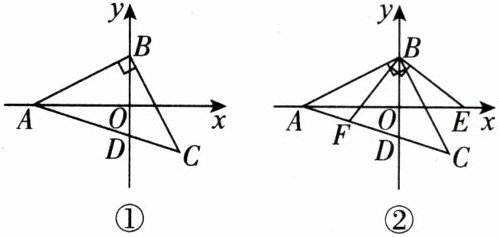
13. [2025武汉江汉区期中]平面直角坐标系中,点$A(a,0)$,$B(0,b)$,$\triangle ABC$为等腰直角三角形,$BA= BC$,$\angle ABC= 90^{\circ }$,$AC交y轴负半轴于点D$。
(1)如图①,$a$,$b满足关系式|a+2b|+(b-2)^{2}= 0$,直接写出点$A$,$B$,$C$的坐标；
(2)如图②,点$E是x$轴正半轴上的动点,过点$B作BF\perp BE交AC于点F$,且$BF= BE$。试说明：点$D是CF$的中点；
(3)在(2)的条件下,$\frac {S_{\triangle FBD}}{S_{\triangle ABE}}$的值是否为定值？若是,请计算出定值；若不是,请用含有$a$,$b$的代数式表示。

答案：
[解]
(1)A(−4,0)，B(0,2)，C(2,−2)。[点拨]因为|a + 2b| + (b−2)² = 0，
所以a + 2b = 0，b−2 = 0，所以b = 2，a = −4。
因为A(a,0)，B(0,b)，所以A(−4,0)，B(0,2)。所以BO = 2，AO = 4。
如图①，过点C作CM⊥y轴交y轴于点M，
所以∠MBC + ∠MCB = 90°。
因为∠ABC = 90°，所以∠MBC + ∠ABM = 90°，
所以∠MCB = ∠ABM，
因为BA = BC，∠AOB = ∠BMC = 90°，
所以△AOB≌△BMC(AAS)，
所以MC = BO = 2，BM = AO = 4，
所以MO = BM−BO = 4−2 = 2，
所以C(2,−2)。
　　　
(2)如图②，过点F作FN⊥y轴交y轴于点N，过点C作CM⊥y轴交y轴于点M。
因为BF⊥BE，所以∠BFN = 90°−∠FBD = ∠EBO。
因为BF = BE，∠BNF = ∠BOE = 90°，
所以△FNB≌△BOE(AAS)，所以FN = BO。
易证△AOB≌△BMC，所以BO = MC，所以FN = MC。
因为∠FND = ∠CMD = 90°，∠FDN = ∠CDM，
所以△FND≌△CMD(AAS)，
所以DF = DC，所以点D是CF的中点。
(3)是定值，为1/2，理由如下：因为A(a,0)，B(0,b)，所以AO = −a，BO = b。
由
(2)知，FN = BO = b，△FND≌△CMD，△FNB≌△BOE，△AOB≌△BMC，所以DN = DM，BN = EO，BM = AO = −a。
设DN = DM = x，所以OE = BN = BM−2x = −a−2x，
所以S△ABE = 1/2AE×BO = 1/2(AO + OE)×b = 1/2(−a−a−2x)×b = −b(a + x)，S△FBD = 1/2BD×FN = 1/2(BM−DM)×b = −1/2b(a + x)，
所以S△FBD/S△ABE = (−1/2b(a + x))/(-b(a + x)) = 1/2。