第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
15. (8分)计算:$\sqrt{\frac{1}{9}} - \sqrt[3]{\frac{26}{27} - 1} + |\sqrt{3} - 2| - (- 2)^2 + 2\sqrt{3}$.
答案:
【解】原式$=\dfrac {1}{3}+\dfrac {1}{3}+2-\sqrt {3}-4+2\sqrt {3}=\sqrt {3}-\dfrac {4}{3}$.
16. (8分)已知实数$a,b$互为相反数,$c,d$互为倒数,$x的绝对值为\sqrt{3}$,求式子$x^2 + (a + b + cd)x + \sqrt{a + b} + \sqrt[3]{cd}$的值.
答案:
【解】因为$a$,$b$互为相反数,$c$,$d$互为倒数,$x$的绝对值为$\sqrt {3}$,所以$a+b=0$,$cd=1$,$x=\pm \sqrt {3}$.
当$x=\sqrt {3}$时,原式$=3+(0+1)\times \sqrt {3}+0+1=4+\sqrt {3}$;
当$x=-\sqrt {3}$时,原式$=3+(0+1)\times (-\sqrt {3})+0+1=4-\sqrt {3}$.
当$x=\sqrt {3}$时,原式$=3+(0+1)\times \sqrt {3}+0+1=4+\sqrt {3}$;
当$x=-\sqrt {3}$时,原式$=3+(0+1)\times (-\sqrt {3})+0+1=4-\sqrt {3}$.
17. (12分)新考法 过程辨析法 先化简,再求值:$a + \sqrt{1 - 2a + a^2}$,其中$a = 1007$.下面是小亮和小芳的解答过程.

解:原式$= a + \sqrt{(1 - a)^2}$
$= a + 1 - a = 1$.
小亮
解:原式$= a + \sqrt{(1 - a)^2}$
$= a + a - 1 = 2013$.
小芳
(1)
(2)错误的原因在于未能正确地运用性质:
(3)先化简,再求值:$a + 2\sqrt{a^2 - 6a + 9}$,其中$a = - 2026$.
解:原式$=a+2\sqrt{(a-3)^2}$
$=-2026+2\sqrt{(-2026-3)^2}$
因为$-2026-3<0$,所以原式$=-2026-2×(-2026-3)$
$=-2026+4052+6$
$=2032$

解:原式$= a + \sqrt{(1 - a)^2}$
$= a + 1 - a = 1$.
小亮
解:原式$= a + \sqrt{(1 - a)^2}$
$= a + a - 1 = 2013$.
小芳
(1)
小亮
的解法是错误的;(2)错误的原因在于未能正确地运用性质:
$\sqrt{a^2}=-a(a<0)$
;(3)先化简,再求值:$a + 2\sqrt{a^2 - 6a + 9}$,其中$a = - 2026$.
解:原式$=a+2\sqrt{(a-3)^2}$
$=-2026+2\sqrt{(-2026-3)^2}$
因为$-2026-3<0$,所以原式$=-2026-2×(-2026-3)$
$=-2026+4052+6$
$=2032$
答案:
【解】(1)小亮 【点拨】当$a=1\ 007$时,原式$=a+\sqrt {(1-a)^{2}}=1\ 007+\sqrt {(1-1\ 007)^{2}}$.因为$1-1\ 007<0$,所以原式$=1\ 007-(1-1\ 007)=1\ 007-1+1\ 007=2\ 013$,所以小亮的解法是错误的.
(2)$\sqrt {a^{2}}=-a(a<0)$
(3)当$a=-2\ 026$时,原式$=a+2\sqrt {(a-3)^{2}}=-2\ 026+2\sqrt {(-2\ 026-3)^{2}}$.因为$-2\ 026-3<0$,所以原式$=-2\ 026-2\times (-2\ 026-3)=-2\ 026+4\ 052+6=2\ 032$.
(2)$\sqrt {a^{2}}=-a(a<0)$
(3)当$a=-2\ 026$时,原式$=a+2\sqrt {(a-3)^{2}}=-2\ 026+2\sqrt {(-2\ 026-3)^{2}}$.因为$-2\ 026-3<0$,所以原式$=-2\ 026-2\times (-2\ 026-3)=-2\ 026+4\ 052+6=2\ 032$.
18. (12分)阅读下面的文字,解答问题:大家知道$\sqrt{2}$是无理数,而无理数是无限不循环小数,因此$\sqrt{2}$的小数部分我们不可能全部写出来.将这个数减去其整数部分,差就是小数部分,因为$\sqrt{2}$的整数部分是1,所以用$\sqrt{2} - 1来表示\sqrt{2}$的小数部分.
例如:因为$\sqrt{4} < \sqrt{6} < \sqrt{9}$,即$2 < \sqrt{6} < 3$,所以$\sqrt{6}$的整数部分是2,小数部分为$\sqrt{6} - 2$.
(1)$\sqrt{23}$的整数部分是______
(2)点$A$表示的数为无理数,在数轴上的位置如图所示,若其整数部分为$m$,小数部分为$n$,则下列对于$m,n$的说法正确的是(
①$m,n$均为有理数;②$1 < \sqrt{m} < 2$;③$3 < m - n < 4$;④$3 < m + n < 4$.
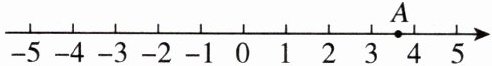
(3)若$p,q分别是6 - \sqrt{5}$的整数部分和小数部分,求$3p - q - \sqrt{5}$的值.
例如:因为$\sqrt{4} < \sqrt{6} < \sqrt{9}$,即$2 < \sqrt{6} < 3$,所以$\sqrt{6}$的整数部分是2,小数部分为$\sqrt{6} - 2$.
(1)$\sqrt{23}$的整数部分是______
4
,小数部分是______$\sqrt{23}-4$
.(2)点$A$表示的数为无理数,在数轴上的位置如图所示,若其整数部分为$m$,小数部分为$n$,则下列对于$m,n$的说法正确的是(
②④
).(填序号)①$m,n$均为有理数;②$1 < \sqrt{m} < 2$;③$3 < m - n < 4$;④$3 < m + n < 4$.
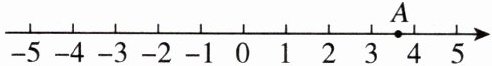
(3)若$p,q分别是6 - \sqrt{5}$的整数部分和小数部分,求$3p - q - \sqrt{5}$的值.
6
答案:
【解】(1)$4$;$\sqrt {23}-4$
(2)②④ 【点拨】设点$A$所表示的无理数为$a$,由题意可知,$3\lt a<4$,所以点$A$所表示的无理数$a$的整数部分$m=3$,小数部分$n=a-3$,因此①$m$,$n$均为有理数,不正确;②由于$1<\sqrt {3}<2$,即$1<\sqrt {m}<2$,因此②正确;③因为$3\lt a<4$,而$m-n=3-a+3=6-a$,所以$2\lt m-n<3$,因此③不正确;④因为$3\lt a<4$,而$m+n=3+a-3=a$,所以$3\lt m+n<4$,因此④正确.综上所述,正确的是②④.
(3)因为$\sqrt {4}<\sqrt {5}<\sqrt {9}$,即$2<\sqrt {5}<3$,所以$-3<-\sqrt {5}<-2$,所以$3<6-\sqrt {5}<4$,所以$6-\sqrt {5}$的整数部分$p=3$,小数部分$q=6-\sqrt {5}-3=3-\sqrt {5}$,所以$3p-q-\sqrt {5}=9-(3-\sqrt {5})-\sqrt {5}=6$.
(2)②④ 【点拨】设点$A$所表示的无理数为$a$,由题意可知,$3\lt a<4$,所以点$A$所表示的无理数$a$的整数部分$m=3$,小数部分$n=a-3$,因此①$m$,$n$均为有理数,不正确;②由于$1<\sqrt {3}<2$,即$1<\sqrt {m}<2$,因此②正确;③因为$3\lt a<4$,而$m-n=3-a+3=6-a$,所以$2\lt m-n<3$,因此③不正确;④因为$3\lt a<4$,而$m+n=3+a-3=a$,所以$3\lt m+n<4$,因此④正确.综上所述,正确的是②④.
(3)因为$\sqrt {4}<\sqrt {5}<\sqrt {9}$,即$2<\sqrt {5}<3$,所以$-3<-\sqrt {5}<-2$,所以$3<6-\sqrt {5}<4$,所以$6-\sqrt {5}$的整数部分$p=3$,小数部分$q=6-\sqrt {5}-3=3-\sqrt {5}$,所以$3p-q-\sqrt {5}=9-(3-\sqrt {5})-\sqrt {5}=6$.
查看更多完整答案,请扫码查看


