第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 勾股定理是数学定理中证明方法最多的定理之一,也是用代数思想解决几何问题最重要的工具之一.下列图形中可以证明勾股定理的有(
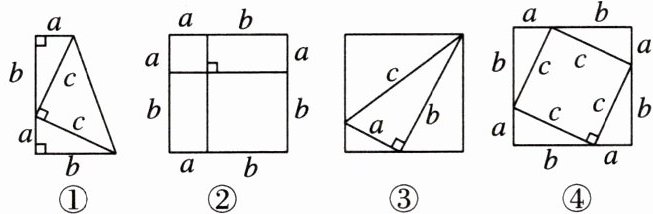
A. ①③
B. ②③
C. ②④
D. ①④
D
)
A. ①③
B. ②③
C. ②④
D. ①④
答案:
D
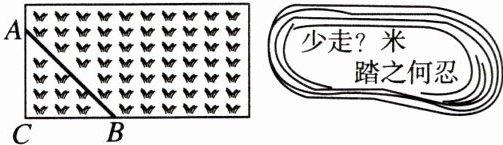
2. 如图是一块长方形草坪,AB是一条被踩踏的小路,已知AC= 12米,BC= 9米.为了避免行人继续踩踏草坪(走线段AB),小梅分别在A,B处各挂了一块下面的牌子,则牌子上“?”处是(
A. 3
B. 4
C. 5
D. 6
D
)
A. 3
B. 4
C. 5
D. 6
答案:
D
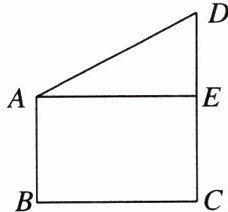
3. 航天科技 2024年11月4日,神舟十八号载人飞船返回舱在东风着陆场成功着陆.为此,某校组织了一次以“指尖上的航模·蓝天下的梦想”为主题的航模飞行表演.如图,小烨控制的无人机在距离地面18米高的点D处(CD= 18米),空中点A处有一只风筝,无人机上的测距仪测得AD= 17米,点A与点D之间的水平距离AE= 15米,已知AE⊥CD于点E,AB= CE,则风筝离地面的高度AB是
10米
.
答案:
10米
4. 意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,其中图①的空白部分由两个正方形和两个直角三角形组成,图②的空白部分由两个直角三角形和一个正方形组成.设图①中空白部分的面积为$S_1,$图②中空白部分的面积为$S_2.$
(1)请用含a,b,c的代数式分别表示$S_1,S_2;$
$S_1=$
(2)请利用达·芬奇的方法验证勾股定理.
由题意得
所以
(1)请用含a,b,c的代数式分别表示$S_1,S_2;$
$S_1=$
$a^{2}+b^{2}+ab$
,$S_2=$$c^{2}+ab$
。(2)请利用达·芬奇的方法验证勾股定理.
由题意得
$S_{1}=S_{2}$
,所以$a^{2}+b^{2}+ab=c^{2}+ab$
。所以
$a^{2}+b^{2}=c^{2}$
。
答案:
【解】
(1)$S_{1}=a^{2}+b^{2}+2×\frac {1}{2}ab=a^{2}+b^{2}+ab$,
$S_{2}=c^{2}+2×\frac {1}{2}ab=c^{2}+ab$。
(2)由题意得$S_{1}=S_{2}$,所以$a^{2}+b^{2}+ab=c^{2}+ab$。
所以$a^{2}+b^{2}=c^{2}$。
(1)$S_{1}=a^{2}+b^{2}+2×\frac {1}{2}ab=a^{2}+b^{2}+ab$,
$S_{2}=c^{2}+2×\frac {1}{2}ab=c^{2}+ab$。
(2)由题意得$S_{1}=S_{2}$,所以$a^{2}+b^{2}+ab=c^{2}+ab$。
所以$a^{2}+b^{2}=c^{2}$。
5. 如图,已知钓鱼竿AC的长为10m,露在水上的鱼线BC长为6m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'的长度为8m,若A,B,B'三点在同一直线上,则BB'的长为(

A. 4m
B. 3m
C. 2m
D. 1m
C
)
A. 4m
B. 3m
C. 2m
D. 1m
答案:
C
6. 一辆装满货物、宽为1.6米的卡车,欲通过如图所示的隧道(隧道上半部分是以AB为直径的半圆),则卡车的高度必须低于(

A. 3.0米
B. 2.9米
C. 2.8米
D. 2.7米
B
)
A. 3.0米
B. 2.9米
C. 2.8米
D. 2.7米
答案:
B
查看更多完整答案,请扫码查看


