第128页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. [2025南京四中月考]某篮球兴趣小组9名学生参加投篮比赛,每人投10个,投中的个数分别为5,8,5,7,5,8,6,5,8,则这组数据的众数为(
A. 8
B. 6
C. 7
D. 5
D
)A. 8
B. 6
C. 7
D. 5
答案:
D
2. 母题教材P147随堂练习T1 巴黎奥运会女子双人10米跳台跳水金牌赛,中国组合五次跳水的成绩(单位:分)分别是56.4,54.6,80.1,85.44,82.56,则她们跳水的平均成绩是(
A. 70.82分
B. 71.82分
C. 72.05分
D. 75.12分
B
)A. 70.82分
B. 71.82分
C. 72.05分
D. 75.12分
答案:
B
3. 新考法方程思想 若一组数据2,3,5,x,7的平均数是4,则x的值为(
A. 4
B. 3
C. 6
D. 5
B
)A. 4
B. 3
C. 6
D. 5
答案:
B
4. 母题教材P147操作·思考 立夏是二十四节气中的第七个节气,是夏季的第一个节气.如图是某地立夏后某一周的每日最高气温折线统计图,则这一周每日最高气温的众数是(
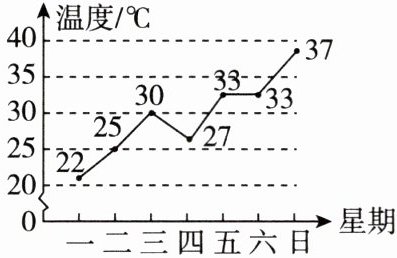
A. $35^{\circ}C$
B. $33^{\circ}C$
C. $30^{\circ}C$
D. 没有众数
B
)
A. $35^{\circ}C$
B. $33^{\circ}C$
C. $30^{\circ}C$
D. 没有众数
答案:
B
5. 小杭同学将自己前7次体育模拟测试成绩统计如表,第8次测试的成绩为a分,若这8次成绩的众数不止一个,则a的值为(
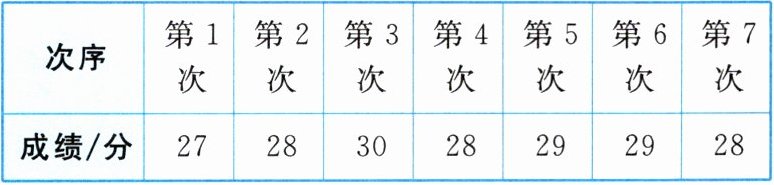
A. 27
B. 28
C. 29
D. 30
C
)
A. 27
B. 28
C. 29
D. 30
答案:
C
6. 若x,y,z的平均数是6,则$5x + 3$,$5y - 2$,$5z + 5$的平均数是(
A. 6
B. 30
C. 33
D. 32
32
)A. 6
B. 30
C. 33
D. 32
答案:
【点拨】因为 $x,y,z$ 的平均数是 6,所以 $x + y + z = 18$。所以 $(5x + 3 + 5y - 2 + 5z + 5) \div 3 = [5(x + y + z) + 6] \div 3 = (5 \times 18 + 6) \div 3 = 32$。
7. 随机抽取某理发店一周的日营业额如下表(单位:元):

如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.

如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
不合理。用该店本周期一到星期日的日平均营业额估计当月的营业总额。$30 × (7560 ÷ 7) = 32400$(元)。所以估计该店当月(按 30 天计算)的营业总额为 32400 元。
答案:
【解】不合理。
用该店本周期一到星期日的日平均营业额估计当月的营业总额。
$30 \times (7560 \div 7) = 32400$(元)。
所以估计该店当月(按 30 天计算)的营业总额为 32400 元。
用该店本周期一到星期日的日平均营业额估计当月的营业总额。
$30 \times (7560 \div 7) = 32400$(元)。
所以估计该店当月(按 30 天计算)的营业总额为 32400 元。
8. 新考法整体代入法 若$x_{1}$,$x_{2}$,…,$x_{5}$的平均数为m;$x_{6}$,$x_{7}$,…,$x_{21}$的平均数为n.则$x_{1}$,$x_{2}$,…,$x_{21}$的平均数为(
A. $m + n$
B. $\frac{m + n}{2}$
C. $\frac{5m + 21n}{21}$
D. $\frac{5m + 16n}{21}$
$\frac{5m + 16n}{21}$
)A. $m + n$
B. $\frac{m + n}{2}$
C. $\frac{5m + 21n}{21}$
D. $\frac{5m + 16n}{21}$
答案:
D 【点拨】因为 $x_1,x_2,\cdots,x_5$ 的平均数为 $m$;$x_6,x_7,\cdots,x_{21}$ 的平均数为 $n$,所以 $x_1 + x_2 + x_3 + x_4 + x_5 = 5m$,$x_6 + x_7 + \cdots + x_{21} = 16n$。所以 $x_1 + x_2 + x_3 + \cdots + x_{21} = 5m + 16n$。所以 $(x_1 + x_2 + x_3 + \cdots + x_{21}) \div 21 = \frac{5m + 16n}{21}$。所以 $x_1,x_2,\cdots,x_{21}$ 的平均数是 $\frac{5m + 16n}{21}$。
9. [2025宁波鄞州区期末]游泳池的水质要求是三次检测的PH的平均值不小于7.2,且不大于7.8.已知某游泳池第一次PH检测值为7.4,第二次PH检测值在7.0至7.9之间(包含7.0和7.9),若该游泳池的水质检测合格,则第三次PH检测值x的范围是(
A. $7.2\leqslant x\leqslant 8.1$
B. $7.1\leqslant x\leqslant 8.0$
C. $7.2\leqslant x\leqslant 8.0$
D. $7.1\leqslant x\leqslant 8.1$
A
)A. $7.2\leqslant x\leqslant 8.1$
B. $7.1\leqslant x\leqslant 8.0$
C. $7.2\leqslant x\leqslant 8.0$
D. $7.1\leqslant x\leqslant 8.1$
答案:
A
查看更多完整答案,请扫码查看


