第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 如图,在四边形ABCD中,$∠D= ∠ACB= 90^{\circ }$,$CD= 12$,$AD= 16$,$BC= 15$,则AB的长为(

A. 20
B. 25
C. 35
D. 30
B
)
A. 20
B. 25
C. 35
D. 30
答案:
B
2. 如图,在长方形ABCD中,$AB= 4cm$,$AD= 12cm$,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长度为(

A. 3 cm
B. 4 cm
C. $\frac {16}{3}cm$
D. $\frac {20}{3}cm$
C
)
A. 3 cm
B. 4 cm
C. $\frac {16}{3}cm$
D. $\frac {20}{3}cm$
答案:
C
3. [2025烟台期中]有一个边长为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形,如图①,其中三个正方形围成的三角形是直角三角形;再经过一次“生长”后,如图②.如果继续“生长”下去,它将变得“枝繁叶茂”,请你计算“生长”了10次后的图形中所有正方形的面积之和为(

A. 11
B. 55
C. 66
D. $2^{11}-1$
A
)
A. 11
B. 55
C. 66
D. $2^{11}-1$
答案:
A
4. 下列由三条线段a,b,c构成的三角形ABC中:①$∠A+∠B= ∠C$;②$a= 3k$,$b= 4k$,$c= 5k(k>0)$;③$∠A:∠B:∠C= 3:4:5$;④$a= m^{2}+1$,$b= m^{2}-1$,$c= 2m$(m为大于1的整数),其中是直角三角形的是(
A. ①④
B. ①②④
C. ②③④
D. ①②③
B
)A. ①④
B. ①②④
C. ②③④
D. ①②③
答案:
B
5. 如图,在$4×4$的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则下列结论错误的是(
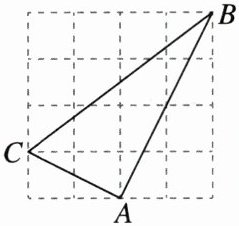
A. $AB^{2}= 20$
B. $∠BAC= 90^{\circ }$
C. $\triangle ABC$的面积为10
D. 点A到直线BC的距离是2
C
)
A. $AB^{2}= 20$
B. $∠BAC= 90^{\circ }$
C. $\triangle ABC$的面积为10
D. 点A到直线BC的距离是2
答案:
C
6. 如图,在四边形ABDC中,$∠A= 90^{\circ }$,$AB= 6$,$AC= 8$,$BD= 5$,$CD^{2}= 125$.
(1)连接BC,求BC的长;
(2)求$\triangle BCD$的面积.

(1)连接BC,求BC的长;
10
(2)求$\triangle BCD$的面积.
25

答案:
【解】
(1)因为在$\triangle ABC$中,$\angle A = 90^{\circ}$,$AB = 6$,$AC = 8$,所以$BC^{2} = AB^{2} + AC^{2} = 100$,所以$BC = 10$。
(2)因为$BC = 10$,$BD = 5$,$CD^{2} = 125$,所以$BC^{2} + BD^{2} = 10^{2} + 5^{2} = 125 = CD^{2}$,所以$\triangle BCD$是直角三角形,且$\angle CBD = 90^{\circ}$,所以$\triangle BCD$的面积为$\frac{1}{2}BD \cdot BC = \frac{1}{2} \times 5 \times 10 = 25$。
(1)因为在$\triangle ABC$中,$\angle A = 90^{\circ}$,$AB = 6$,$AC = 8$,所以$BC^{2} = AB^{2} + AC^{2} = 100$,所以$BC = 10$。
(2)因为$BC = 10$,$BD = 5$,$CD^{2} = 125$,所以$BC^{2} + BD^{2} = 10^{2} + 5^{2} = 125 = CD^{2}$,所以$\triangle BCD$是直角三角形,且$\angle CBD = 90^{\circ}$,所以$\triangle BCD$的面积为$\frac{1}{2}BD \cdot BC = \frac{1}{2} \times 5 \times 10 = 25$。
7. 新考向数学文化法国数学家费尔马早在17世纪就研究过形如$x^{2}+y^{2}= z^{2}$的方程,显然,这个方程有无数组解.我们把满足该方程的正整数的解$(x,y,z)$称为勾股数.如$(3,4,5)$就是一组勾股数.
(1)请你再写出两组勾股数:
(2)在研究直角三角形的勾股数时,古希腊哲学家柏拉图曾指出:如果n表示大于1的整数,$x= 2n$,$y= n^{2}-1$,$z= n^{2}+1$,那么以x,y,z为三边长的三角形为直角三角形,即$(x,y,z)$为勾股数.请你加以说明.
(1)请你再写出两组勾股数:
$(6,8,10)$
,$(9,12,15)$
;(2)在研究直角三角形的勾股数时,古希腊哲学家柏拉图曾指出:如果n表示大于1的整数,$x= 2n$,$y= n^{2}-1$,$z= n^{2}+1$,那么以x,y,z为三边长的三角形为直角三角形,即$(x,y,z)$为勾股数.请你加以说明.
答案:
【解】
(1)$(6,8,10)$;$(9,12,15)$(答案不唯一)
(2)因为$x^{2} + y^{2} = (2n)^{2} + (n^{2} - 1)^{2} = 4n^{2} + n^{4} - 2n^{2} + 1 = n^{4} + 2n^{2} + 1 = (n^{2} + 1)^{2} = z^{2}$,所以$(x,y,z)$为勾股数。
(1)$(6,8,10)$;$(9,12,15)$(答案不唯一)
(2)因为$x^{2} + y^{2} = (2n)^{2} + (n^{2} - 1)^{2} = 4n^{2} + n^{4} - 2n^{2} + 1 = n^{4} + 2n^{2} + 1 = (n^{2} + 1)^{2} = z^{2}$,所以$(x,y,z)$为勾股数。
查看更多完整答案,请扫码查看


