《2025年综合应用创新题典中点八年级数学上册北师大版》

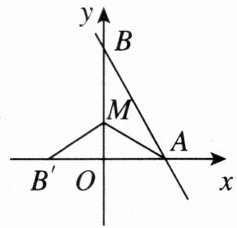
14. [2025深圳罗湖区月考] 如图,直线$AB:y= -\frac {4}{3}x+4$与x轴,y轴分别相交于点A和点B,M是OB上一点,若将$\triangle ABM$沿AM所在直线折叠,点B恰好落在x轴上的点$B'$处,则$\triangle ABM$的面积等于____$\frac{15}{4}$.

答案： $\frac{15}{4}$　[点拨]因为直线AB的表达式为y = - $\frac{4}{3}$x + 4,所以当x = 0时,y = 4,当y = 0时, - $\frac{4}{3}$x + 4 = 0,解得x = 3.所以A(3, 0),B(0, 4).所以OA = 3,OB = 4.所以AB = $\sqrt{3² + 4²}$ = 5.由折叠可知,AB' = AB = 5,S△ABM = S△AB'M,所以$\frac{1}{2}$AB'·OM = $\frac{1}{2}$BM·OA.设M(0,m),则OM = m,所以BM = OB - OM = 4 - m.所以$\frac{1}{2}$×5m = $\frac{1}{2}$×3(4 - m),解得m = $\frac{3}{2}$.所以S△ABM = $\frac{1}{2}$×3×(4 - $\frac{3}{2}$) = $\frac{15}{4}$.

15. 新视角新定义题 定义:对于关于x的一次函数$y= kx+b(k≠0)$,我们称函数$y= \left\{\begin{array}{l} kx+b(x≤a),\\ -kx-b(x＞a)\end{array}\right. 为一次函数y= kx+b(k≠0)$的“a变换函数”(其中a为常数).例如:对于关于x的一次函数$y= 2x+1$的“5变换函数”为$y= \left\{\begin{array}{l} 2x+1(x≤5),\\ -2x-1(x＞5).\end{array}\right. $
(1)一次函数$y= -x+1$的“0变换函数”为$y= $____.
(2)画出一次函数$y= -x+1$的“2变换函数”图象,并完成下列问题:
①对于一次函数$y= -x+1$的“2变换函数”,当$x= 3$时,求y的值;当$y= 2$时,求x的值;
②对于一次函数$y= -x+1$的“2变换函数”,当$-3≤x≤3$时,y的取值范围是____.
(3)当一次函数$y= -x+1$的“a变换函数”图象与直线$y= 2$有一个交点时,直接写出a的取值范围.

答案：
[解]
(1)$\left\{ \begin{array} { l } { - x + 1 ( x \leq 0 ), } \\ { x - 1 ( x ＞ 0 ) } \end{array} \right.$
(2)y = - x + 1的“2变换函数”为y = $\left\{ \begin{array} { l } { - x + 1 ( x \leq 2 ), } \\ { x - 1 ( x ＞ 2 ), } \end{array} \right.$其图象如图所示.
　　　　　　
　①当x = 3时,y = 3 - 1 = 2;
　当y = 2时, - x + 1 = 2或x - 1 = 2,
　解得x = - 1或x = 3.
　② - 1 ≤ y ≤ 4　[点拨]当 - 3 ≤ x ≤ 2时,y = - x + 1,易知y随x的增大而减小.所以 - 1 ≤ y ≤ 4;当2 ＜ x ≤ 3时,y = x - 1,易知y随x的增大而增大,所以1 ＜ y ≤ 2.综上所述， - 1 ≤ y ≤ 4.
(3)当一次函数y = - x + 1的“a变换函数”图象与直线y = 2有一个交点时,a ＜ - 1或a ≥ 3.

16. 新考法分类讨论法 如图,直线$l:y= ax+3$交x轴于点$A(6,0)$,将直线l向下平移4个单位,得到的直线分别交x轴、y轴于点B,C.
(1)求a的值及B,C两点的坐标;
a的值为-$\frac{1}{2}$，B点坐标为(-2,0)，C点坐标为(0,-1)
(2)点M为线段AB上一点,连接CM并延长,交直线l于点N,若$\triangle AMN$是等腰三角形,求点M的坐标.
点M的坐标为(2,0)或($\sqrt{5}$-2,0)或(-$\frac{3}{4}$,0)

答案： [解]
(1)因为直线l:y = ax + 3交x轴于点A(6, 0),所以6a + 3 = 0,解得a = - $\frac{1}{2}$.所以y = - $\frac{1}{2}$x + 3.
　所以平移后的直线为y1 = - $\frac{1}{2}$x + 3 - 4 = - $\frac{1}{2}$x - 1.
　令y1 = 0,则 - $\frac{1}{2}$x - 1 = 0,解得x = - 2.
　令x = 0,则y1 = - 1,所以B( - 2, 0),C(0, - 1).
(2)分情况讨论:若MN = AN,则∠AMN = ∠MAN.
　由题易知AN//BC,所以∠MAN = ∠MBC.所以∠AMN = ∠MBC;又因为∠AMN = ∠BMC,所以∠MBC = ∠BMC.所以BC = CM.
　又因为CO⊥BM,所以OM = OB.
　由
(1)知OB = 2,所以OM = 2.所以M(2, 0);
　若AM = AN,则∠AMN = ∠ANM;
　因为AN//BC,所以∠ANM = ∠BCM.所以∠AMN = ∠BCM.又因为∠AMN = ∠BMC,所以∠BCM = ∠BMC.所以BC = BM;
　由
(1)知B( - 2, 0),C(0, - 1),所以易得BC = $\sqrt{2² + 1²}$ = $\sqrt{5}$.所以BM = $\sqrt{5}$,所以OM = $\sqrt{5}$ - 2.所以M( $\sqrt{5}$ - 2, 0);
　若AM = MN,则∠MAN = ∠ANM.
　因为AN//BC,所以∠MAN = ∠MBC,∠MCB = ∠ANM.所以∠MBC = ∠MCB.所以CM = BM.所以CM² = OC² + OM² = (OB - OM)².易知OC = 1,OB = 2,所以(2 - OM)² = OM² + 1².所以OM = $\frac{3}{4}$.
所以易知M( - $\frac{3}{4}$, 0).
综上，点M的坐标为(2, 0)或( $\sqrt{5}$ - 2, 0)或( - $\frac{3}{4}$, 0).