第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
13. 已知m是$\sqrt[3]{13}$的整数部分,n是$\sqrt{13}$的小数部分,则m-n=
$5-\sqrt{13}$
答案:
$5-\sqrt{13}$
14. 已知$\sqrt[3]{x-1}= x-1$,则$\sqrt{x}$的值为
$\sqrt{2}$或1或0
.
答案:
$\sqrt{2}$或1或0
15. 一个正方形的边长变为原来的8倍后,面积变为原来的a倍;一个正方体的体积变为原来的27倍后,棱长变为原来的b倍,则$-\sqrt{a}的立方根与b^{2}$的平方根的和为
1或-5
.
答案:
1或$-5$ 【点拨】一个正方形的边长变为原来的8倍后,面积变为原来的64倍,即$a=64$,一个正方体的体积变为原来的27倍,则棱长变为原来的3倍,即$b=3$.所以$-\sqrt{a}=-8$,$b^{2}=9$,所以$-\sqrt{a}$的立方根为$-2$,$b^{2}$的平方根为$\pm3$.因为$-2+3=1$,$-2+(-3)=-5$,所以$-\sqrt{a}$的立方根与$b^{2}$的平方根的和为1或$-5$.
16. 已知$|a-1|= 5,(b+2)^{2}= 9,c^{3}= -8$.
(1)求b的值;
(2)若a<b,求a+b的值;
(3)若abc>0,求a-3b-2c的值.
(1)求b的值;
1或-5
(2)若a<b,求a+b的值;
-3
(3)若abc>0,求a-3b-2c的值.
-3或25
答案:
【解】
(1)因为$(b+2)^{2}=9$,所以$b+2=3$或$b+2=-3$,所以$b=1$或$b=-5$.
(2)因为$|a-1|=5$,所以$a-1=5$或$a-1=-5$,所以$a=6$或$a=-4$.因为$a\lt b$,所以$a=-4$,$b=1$,所以$a+b=-4+1=-3$.
(3)因为$c^{3}=-8$,所以$c=-2$.
又因为$abc>0$,所以$ab<0$,即$a$,$b$异号,
所以$b=1$,$a=-4$,或$b=-5$,$a=6$.
当$b=1$,$a=-4$时,$a-3b-2c=-4-3\times1-2\times(-2)=-4-3+4=-3$;
当$b=-5$,$a=6$时,$a-3b-2c=6-3\times(-5)-2\times(-2)=6+15+4=25$.
综上可知,$a-3b-2c$的值为$-3$或25.
(1)因为$(b+2)^{2}=9$,所以$b+2=3$或$b+2=-3$,所以$b=1$或$b=-5$.
(2)因为$|a-1|=5$,所以$a-1=5$或$a-1=-5$,所以$a=6$或$a=-4$.因为$a\lt b$,所以$a=-4$,$b=1$,所以$a+b=-4+1=-3$.
(3)因为$c^{3}=-8$,所以$c=-2$.
又因为$abc>0$,所以$ab<0$,即$a$,$b$异号,
所以$b=1$,$a=-4$,或$b=-5$,$a=6$.
当$b=1$,$a=-4$时,$a-3b-2c=-4-3\times1-2\times(-2)=-4-3+4=-3$;
当$b=-5$,$a=6$时,$a-3b-2c=6-3\times(-5)-2\times(-2)=6+15+4=25$.
综上可知,$a-3b-2c$的值为$-3$或25.
17. 我国著名数学家华罗庚在杂志上看到这样的问题:求59319的立方根.他脱口而出:39.他是怎样快速准确算出来的呢?
(1)【知识储备】开立方与立方互为逆运算,如:因为$0^{3}= 0$,所以$\sqrt[3]{0}= 0$;因为$(-2)^{3}= -8$,所以$\sqrt[3]{-8}= -2$,因此,我们需要熟悉一些数及其立方.请补全表格:
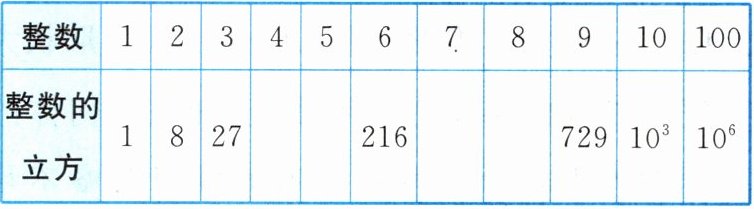
(2)【思路探究】尝试求出19683的立方根是哪个整数:
①确定立方根的位数:由$10^{3}= 1000,100^{3}= 1000000$,确定$\sqrt[3]{19683}$是
②确定个位的数字:根据(1)中各整数的立方的个位数字,确定$\sqrt[3]{19683}$的个位上的数字是
③确定十位的数字:由$20^{3}= 8000,30^{3}= 27000$,且$8000<19683<27000$,确定$\sqrt[3]{19683}$的十位上的数字是
④确定立方根的值:由①~③可得$\sqrt[3]{19683}$的值为
(3)【尝试应用】某商场拟建一个容积为373248的正方体玻璃柜放置东莞迎恩门城楼模型,请问这个正方体玻璃柜的棱长是多少?直接写出答案.
(1)【知识储备】开立方与立方互为逆运算,如:因为$0^{3}= 0$,所以$\sqrt[3]{0}= 0$;因为$(-2)^{3}= -8$,所以$\sqrt[3]{-8}= -2$,因此,我们需要熟悉一些数及其立方.请补全表格:

(2)【思路探究】尝试求出19683的立方根是哪个整数:
①确定立方根的位数:由$10^{3}= 1000,100^{3}= 1000000$,确定$\sqrt[3]{19683}$是
两
位数;②确定个位的数字:根据(1)中各整数的立方的个位数字,确定$\sqrt[3]{19683}$的个位上的数字是
7
;③确定十位的数字:由$20^{3}= 8000,30^{3}= 27000$,且$8000<19683<27000$,确定$\sqrt[3]{19683}$的十位上的数字是
2
;④确定立方根的值:由①~③可得$\sqrt[3]{19683}$的值为
27
.(3)【尝试应用】某商场拟建一个容积为373248的正方体玻璃柜放置东莞迎恩门城楼模型,请问这个正方体玻璃柜的棱长是多少?直接写出答案.
72
答案:
【解】
(1)64;125;343;512
(2)①两 ②7 ③2 ④27
(3)这个正方体玻璃柜的棱长是72.
(1)64;125;343;512
(2)①两 ②7 ③2 ④27
(3)这个正方体玻璃柜的棱长是72.
查看更多完整答案,请扫码查看


