第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
6. 从某容器口以均匀地速度注入酒精,若液面高度h随时间t的变化情况如图所示,则对应容器的形状为(
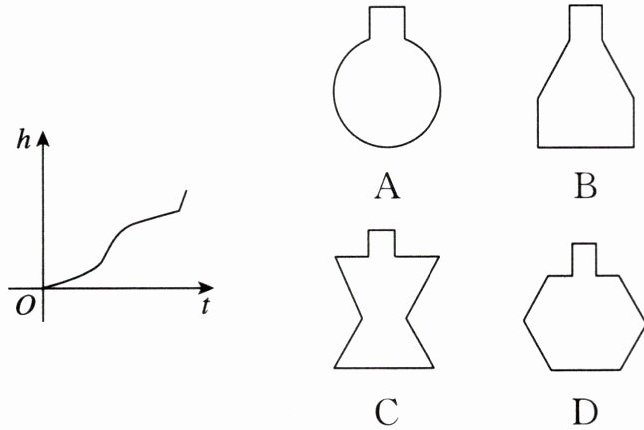
C
)
答案:
C
7. 刘阿姨早晨从家里出发去公园锻炼,匀速走了60min后回到家(中间不休息).如图表示她出发后离家的距离s(单位:km)与行走时间t(单位:min)之间的函数关系.则下列图形中可以大致描述刘阿姨行走路线的是(
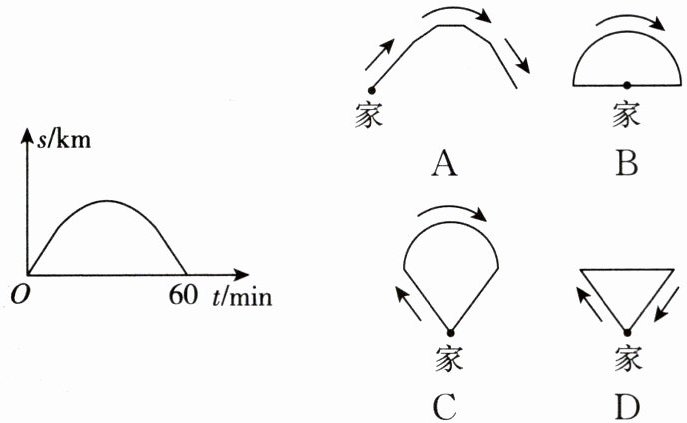
C
)
答案:
C
8. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线).这个容器的形状可能是(
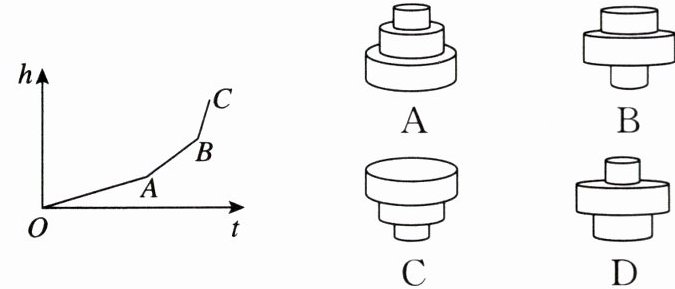
A
)
答案:
A
9. 如图①,小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮离家的距离y(单位:km)与时间x(单位:min)之间的关系如图②所示.下列结论错误的是(
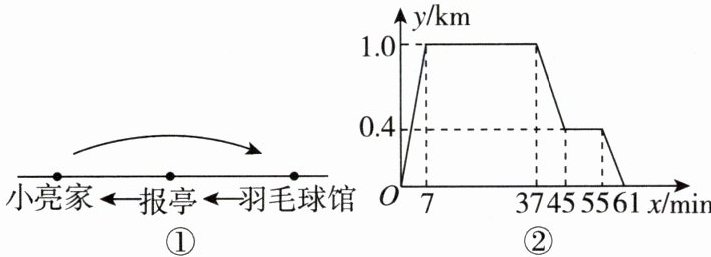
A. 小亮从家到羽毛球馆用了7min
B. 小亮从羽毛球馆到报亭平均每分钟走75m
C. 报亭到小亮家的距离是400m
D. 小亮打羽毛球的时间是37min
D
)
A. 小亮从家到羽毛球馆用了7min
B. 小亮从羽毛球馆到报亭平均每分钟走75m
C. 报亭到小亮家的距离是400m
D. 小亮打羽毛球的时间是37min
答案:
D [点拨]A.由图象得小亮从家到羽毛球馆用了7min,故A选项不符合题意;B.由图象可知小亮从羽毛球馆到报亭的平均速度为(1.0−0.4)÷(45−37)=0.075(km/min)=75(m/min),故B选项不符合题意;C.由图象知报亭到小亮家的距离是0.4km,即400m,故C选项不符合题意;D.由图象知小亮打羽毛球的时间是37−7=30(min),故D选项符合题意。
10. [2024威海]同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从A地、B地同时出发前往C地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.如图表示甲、乙两车之间的距离y(单位:km)与时间x(单位:h)的函数关系.下列结论正确的是( )
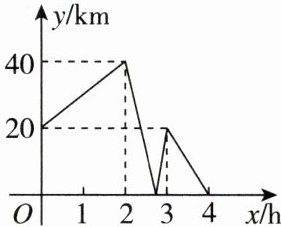
A. 甲车行驶$\frac{8}{3}$h与乙车相遇
B. A,C两地相距220km
C. 甲车的速度是70km/h
D. 乙车中途休息36min

A. 甲车行驶$\frac{8}{3}$h与乙车相遇
B. A,C两地相距220km
C. 甲车的速度是70km/h
D. 乙车中途休息36min
答案:
A [点拨]根据函数图象可得A、B两地之间的距离为20km,两车行驶了4h,同时到达C地,如图所示,在1 - 2h,两车同向运动,在2h,即点D时,两车距离发生改变,此时乙车休息,E点的意义是两车相遇,F点的意义是乙车休息后再出发,所以乙车休息了1h,故D不正确,不符合题意;设甲车的速度为akm/h,乙车的速度为bkm/h,根据题意,乙车休息后两车同时到达C地,则甲车的速度比乙车的速度慢,即a<b。因为2b + 20 - 2a = 40,即b - a = 10,在DE和EF时,乙车不动,则甲车的速度是$\frac{40 + 20}{1} = 60(km/h)$,所以乙车的速度为60 + 10 = 70(km/h),故C不正确,不符合题意;所以A、C两地的距离为4×60 = 240(km),故B不正确,不符合题意;设xh时两车相遇,依题意得60x = 2×70 + 20,解得$x = \frac{8}{3}$,即$\frac{8}{3}$h时,两车相遇,故A正确,符合题意。

A [点拨]根据函数图象可得A、B两地之间的距离为20km,两车行驶了4h,同时到达C地,如图所示,在1 - 2h,两车同向运动,在2h,即点D时,两车距离发生改变,此时乙车休息,E点的意义是两车相遇,F点的意义是乙车休息后再出发,所以乙车休息了1h,故D不正确,不符合题意;设甲车的速度为akm/h,乙车的速度为bkm/h,根据题意,乙车休息后两车同时到达C地,则甲车的速度比乙车的速度慢,即a<b。因为2b + 20 - 2a = 40,即b - a = 10,在DE和EF时,乙车不动,则甲车的速度是$\frac{40 + 20}{1} = 60(km/h)$,所以乙车的速度为60 + 10 = 70(km/h),故C不正确,不符合题意;所以A、C两地的距离为4×60 = 240(km),故B不正确,不符合题意;设xh时两车相遇,依题意得60x = 2×70 + 20,解得$x = \frac{8}{3}$,即$\frac{8}{3}$h时,两车相遇,故A正确,符合题意。

11. 如图①,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为x,$\frac{PB}{PC}= y$,图②是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为( )
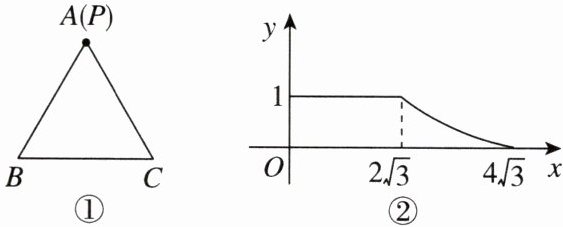
A. 6
B. 3
C. $4\sqrt{3}$
D. $2\sqrt{3}$

A. 6
B. 3
C. $4\sqrt{3}$
D. $2\sqrt{3}$
答案:
A [点拨]如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,结合图象可知,当点P在AO上运动时,$\frac{PB}{PC} = 1$,所以$PB = PC$,$AO = 2\sqrt{3}$。又因为$\triangle ABC$为等边三角形,所以$∠BAC = 60^{\circ}$,$AB = AC$,所以$\triangle APB ≌ \triangle APC(SSS)$。所以$∠BAO = ∠CAO = 30^{\circ}$。当点P在OB上运动时,可知点P到达点B时的路程为$4\sqrt{3}$,所以$OB = 2\sqrt{3}$,即$AO = OB = 2\sqrt{3}$,所以$∠BAO = ∠ABO = 30^{\circ}$。过点O作$OD ⊥ AB$,垂足为D。所以$AD = BD$,易知$AD = 3$,所以$AB = AD + BD = 6$,即等边三角形ABC的边长为6。

A [点拨]如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,结合图象可知,当点P在AO上运动时,$\frac{PB}{PC} = 1$,所以$PB = PC$,$AO = 2\sqrt{3}$。又因为$\triangle ABC$为等边三角形,所以$∠BAC = 60^{\circ}$,$AB = AC$,所以$\triangle APB ≌ \triangle APC(SSS)$。所以$∠BAO = ∠CAO = 30^{\circ}$。当点P在OB上运动时,可知点P到达点B时的路程为$4\sqrt{3}$,所以$OB = 2\sqrt{3}$,即$AO = OB = 2\sqrt{3}$,所以$∠BAO = ∠ABO = 30^{\circ}$。过点O作$OD ⊥ AB$,垂足为D。所以$AD = BD$,易知$AD = 3$,所以$AB = AD + BD = 6$,即等边三角形ABC的边长为6。

查看更多完整答案,请扫码查看


