第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 一个长方形抽屉长20cm,宽30cm,贴抽屉底面放一根木棒,那么这根木棒最长(取整厘米数,不计木棒粗细)可以是 (
A. 30cm
B. 35cm
C. 36cm
D. 37cm
C
)A. 30cm
B. 35cm
C. 36cm
D. 37cm
答案:
C
2. [2025西安未央区开学考试]如图,某自动感应门的正上方A处装着一个感应器,离地2.1米($AB = 2.1$米),当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米($BC = 1.2$米)的地方时,感应门自动打开,则人头顶离感应器的距离AD等于 (
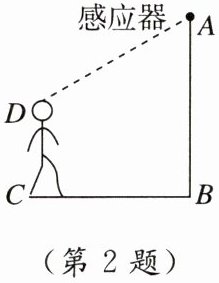
A. 1.2米
B. 1.3米
C. 1.5米
D. 2米
B
)
A. 1.2米
B. 1.3米
C. 1.5米
D. 2米
答案:
B
3. 情境题 生活应用 如图,一扇卷闸门用一块宽50cm,长120cm的长方形木板撑住,用这块木板最多可将这扇卷闸门撑起的高度为
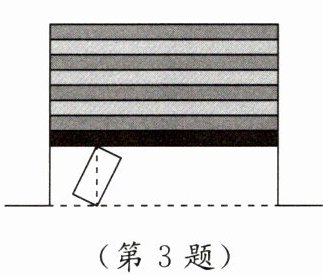
130
cm.
答案:
130
4. 如图所示的人字梯撑开后侧面是一个等腰三角形,若梯子长AB等于2.5m,梯子完全撑开后顶端离地面的高度AD等于2.4m,则此时梯子侧面宽度BC等于
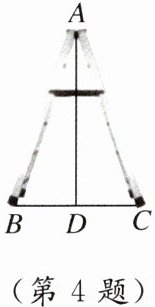
1.4
m.
答案:
1.4
5. 如图,某小区有一块四边形空地ABCD,为了美化小区环境,现计划在空地上铺上草坪,经测量$∠A = 90^{\circ}$,$AB = 20$米,$BC = 24$米,$CD = 7$米,$AD = 15$米.若铺一平方米草坪需要50元,则铺这块空地需要投入资金______
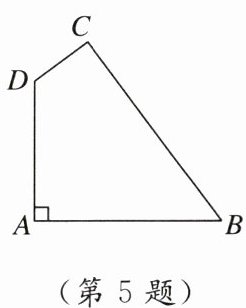
11700
元.
答案:
11700 [点拨]连接BD。
因为∠A = 90°,AB = 20米,AD = 15米,
所以BD² = AD² + AB² = 15² + 20² = 625。
因为BC = 24米,CD = 7米,
所以BC² + CD² = 24² + 7² = 625 = BD²,
所以△BDC是直角三角形,且∠C = 90°,
所以四边形ABCD的面积为S△ABD + S△BCD = $\frac{1}{2}$AB·AD + $\frac{1}{2}$BC·CD = $\frac{1}{2}$×20×15 + $\frac{1}{2}$×24×7 = 150 + 84 = 234(平方米),
所以铺这块空地需要投入资金234×50 = 11700(元)。
因为∠A = 90°,AB = 20米,AD = 15米,
所以BD² = AD² + AB² = 15² + 20² = 625。
因为BC = 24米,CD = 7米,
所以BC² + CD² = 24² + 7² = 625 = BD²,
所以△BDC是直角三角形,且∠C = 90°,
所以四边形ABCD的面积为S△ABD + S△BCD = $\frac{1}{2}$AB·AD + $\frac{1}{2}$BC·CD = $\frac{1}{2}$×20×15 + $\frac{1}{2}$×24×7 = 150 + 84 = 234(平方米),
所以铺这块空地需要投入资金234×50 = 11700(元)。
6. 立德树人 保护森林 爱护森林人人有责,如图(单位:cm)是某森林小队为该地区森林鸟类安装的木屋示意图,它为轴对称图形,求屋顶A到地面BM的距离.
[解]因为木屋为轴对称图形,
所以△ACD是等腰三角形。
作AE⊥CD,垂足为E。
由题意得CD = 30 + 2 = 32(cm),
所以CE = DE = 32×$\frac{1}{2}$ = 16(cm)。
因为AD = 20cm,所以AE² = 20² - 16² = 144。
所以AE = 12cm。
所以屋顶A到地面BM的距离为12 + 12 + 16 =
[解]因为木屋为轴对称图形,
所以△ACD是等腰三角形。
作AE⊥CD,垂足为E。
由题意得CD = 30 + 2 = 32(cm),
所以CE = DE = 32×$\frac{1}{2}$ = 16(cm)。
因为AD = 20cm,所以AE² = 20² - 16² = 144。
所以AE = 12cm。
所以屋顶A到地面BM的距离为12 + 12 + 16 =
40
(cm)。
答案:
[解]因为木屋为轴对称图形,
所以△ACD是等腰三角形。
作AE⊥CD,垂足为E。
由题意得CD = 30 + 2 = 32(cm),
所以CE = DE = 32×$\frac{1}{2}$ = 16(cm)。
因为AD = 20cm,所以AE² = 20² - 16² = 144。
所以AE = 12cm。
所以屋顶A到地面BM的距离为12 + 12 + 16 = 40(cm)。
所以△ACD是等腰三角形。
作AE⊥CD,垂足为E。
由题意得CD = 30 + 2 = 32(cm),
所以CE = DE = 32×$\frac{1}{2}$ = 16(cm)。
因为AD = 20cm,所以AE² = 20² - 16² = 144。
所以AE = 12cm。
所以屋顶A到地面BM的距离为12 + 12 + 16 = 40(cm)。
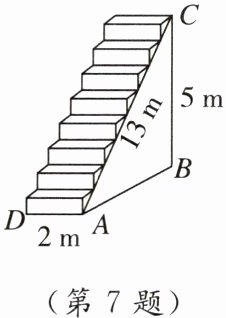
7. 新考法 平移法 如图,某会展中心在会展期间准备将高5m、长13m、宽2m的楼梯铺上地毯,已知地毯每平方米30元,请你帮忙计算一下,铺完这个楼梯至少需要
1020
元.
答案:
1020 [点拨]由勾股定理得AB² = AC² - BC² = 13² - 5² = 144,所以AB = 12m,所以地毯总长为12 + 5 = 17(m),所以地毯的总面积为17×2 = 34(m²),所以铺完这个楼梯至少需要34×30 = 1020(元)。
8. [2025淄博期中]我国古代数学著作《九章算术》第九章《勾股》中记载了这样的一个问题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门AD和BC,门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB是______寸(1尺= 10寸).


答案:
101 [点拨]如图,过点D作DE⊥AB于点E。设OA = OB = AD = BC = r寸。由题意得DE = 1尺 = 10寸,OE = $\frac{1}{2}$CD = 1寸,则AE = (r - 1)寸。在Rt△ADE中,AE² + DE² = AD²,即(r - 1)² + 10² = r²,

解得r = 50.5,所以AB = 2r = 101寸。
101 [点拨]如图,过点D作DE⊥AB于点E。设OA = OB = AD = BC = r寸。由题意得DE = 1尺 = 10寸,OE = $\frac{1}{2}$CD = 1寸,则AE = (r - 1)寸。在Rt△ADE中,AE² + DE² = AD²,即(r - 1)² + 10² = r²,

解得r = 50.5,所以AB = 2r = 101寸。
查看更多完整答案,请扫码查看


