第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
8. 七年级某班有48名学生,所在教室有6行8列座位,用$(m,n)$表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为$(m,n)$,若调整后的座位为$(i,j)$,则称该生作了平移$[a,b]= [m-i,n-j]$,并称$a+b$为该生的位置数.某生的位置数为8,当$m+n$取最小值时,则mn的最大值为(
A. 25
B. 30
C. 36
D. 48
A
)A. 25
B. 30
C. 36
D. 48
答案:
A [点拨]因为$[a,b]=[m - i,n - j]$,所以$a + b=m - i+n - j=m + n-(i + j)$。又因为$a + b = 8$,所以$m + n-(i + j)=8$,即$m + n=i + j + 8$。因为$1\leq i\leq6$,$1\leq j\leq8$,且i,j都是整数,所以$m + n$的最小值为10。当$m = 2$,$n = 8$时,$mn = 16$;当$m = 3$,$n = 7$时,$mn = 21$;当$m = 4$,$n = 6$时,$mn = 24$;当$m = 5$,$n = 5$时,$mn = 25$;当$m = 6$,$n = 4$时,$mn = 24$,所以$mn$的最大值为25,故选A。
9. 根据格子图填空.
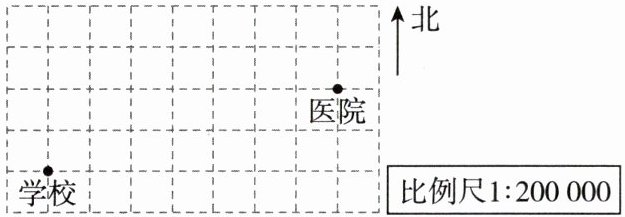
(1)如果学校的位置用数对$(0,0)$表示,那么医院的位置应用数对(
(2)经测量学校到医院的图上距离约为
(3)医院位于学校的

(1)如果学校的位置用数对$(0,0)$表示,那么医院的位置应用数对(
7
,2
)表示;(2)经测量学校到医院的图上距离约为
3.2
cm(保留一位小数),实际距离约是6.4
km;(3)医院位于学校的
北偏东74°
方向上(用量角器测量角度,精确到$1^{\circ }$).
答案:
(1)7;2
(2)3.2,6.4
(3)北偏东$74^{\circ}$
(1)7;2
(2)3.2,6.4
(3)北偏东$74^{\circ}$
10. [2025上海浦东新区期中]如图,在$5×5$的方格(每个小正方形的边长为1)内有1只甲虫,它爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:$A→B(+1,+4)$,从B到A的爬行路线为:$B→A(-1,-4)$,其中第一个数表示左右爬行信息,第二个数表示上下爬行信息.
(1)图中$B→D$(____,____),$C→B(-2$,____);
(2)若甲虫的爬行路线为$A→B→C→D$,计算甲虫爬行的路程.
(3)若甲虫从点A出发,爬行路线依次为$(+2,+3),(-2,+1),(+3,-5),(-4,+2)$,最终到达点P处,请在图中标出点P的位置.
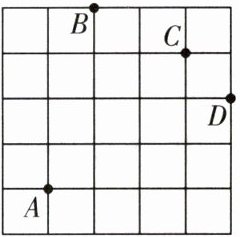
(1)图中$B→D$(____,____),$C→B(-2$,____);
(2)若甲虫的爬行路线为$A→B→C→D$,计算甲虫爬行的路程.
(3)若甲虫从点A出发,爬行路线依次为$(+2,+3),(-2,+1),(+3,-5),(-4,+2)$,最终到达点P处,请在图中标出点P的位置.

答案:
[解]
(1)$+3;-2;+1$
(2)由A到B的爬行路线为$(+1,+4)$,由B到C的爬行路线为$(+2,-1)$,由C到D的爬行路线为$(+1,-1)$,所以甲虫爬行的路程为$1 + 2+1 + 4+1 + 1 = 10$。
(3)如图,点P即为所求.

[解]
(1)$+3;-2;+1$
(2)由A到B的爬行路线为$(+1,+4)$,由B到C的爬行路线为$(+2,-1)$,由C到D的爬行路线为$(+1,-1)$,所以甲虫爬行的路程为$1 + 2+1 + 4+1 + 1 = 10$。
(3)如图,点P即为所求.

11. 新趋势 学科内综合 如图①,将射线OX按逆时针方向旋转$\beta ^{\circ }$,得到射线OY,如果点P为射线OY上的一点,且$OP= a$,那么我们规定用$(a,\beta )$表示点P在平面内的位置,并记为$P(a,\beta )$,例如,在图②中,如果$OM= 8,∠XOM= 110^{\circ }$,那么点M在平面内的位置记为$M(8,110)$,根据图形,解答下面的问题:
(1)如图③,如果点N在平面内的位置记为$N(6,30)$,那么$ON= $____,$∠XON= $____;
(2)如果点A,B在平面内的位置分别记为$A(5,30),B(12,120)$,求A,B两点之间的距离,并
画出图.
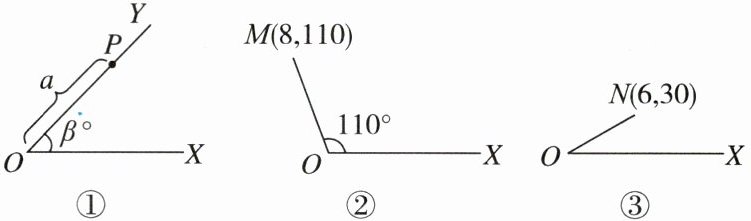
(1)如图③,如果点N在平面内的位置记为$N(6,30)$,那么$ON= $____,$∠XON= $____;
(2)如果点A,B在平面内的位置分别记为$A(5,30),B(12,120)$,求A,B两点之间的距离,并
画出图.

答案:
[解]
(1)6;$30^{\circ}$
(2)如图所示,因为$A(5,30)$,$B(12,120)$,所以$∠BOX = 120^{\circ}$,$∠AOX = 30^{\circ}$,$OA = 5$,$OB = 12$,所以$∠AOB = 90^{\circ}$,所以在$Rt△AOB$中,$AB=\sqrt{12^{2}+5^{2}} = 13$。

[解]
(1)6;$30^{\circ}$
(2)如图所示,因为$A(5,30)$,$B(12,120)$,所以$∠BOX = 120^{\circ}$,$∠AOX = 30^{\circ}$,$OA = 5$,$OB = 12$,所以$∠AOB = 90^{\circ}$,所以在$Rt△AOB$中,$AB=\sqrt{12^{2}+5^{2}} = 13$。

查看更多完整答案,请扫码查看


