《2025年综合应用创新题典中点八年级数学上册北师大版》

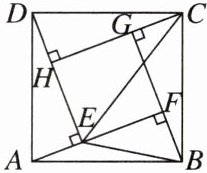
7. [2025盐城期中]第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH拼成的大正方形ABCD中,连接BE,CE.若△CDE的面积是△ABE面积的9倍,小正方形EFGH的面积是16,则大正方形ABCD的面积为______40.

答案： 40　【点拨】设$AE=BF=a$，$DE=AF=CH=b(b＞a＞0)$。由题意得$S_{△CDE}=\frac {1}{2}DE\cdot CH=\frac {1}{2}b^{2}$，$S_{△AEB}=\frac {1}{2}AE\cdot BF=\frac {1}{2}a^{2}$。因为$△CDE$的面积是$△ABE$面积的9倍，所以$\frac {1}{2}b^{2}=\frac {9}{2}a^{2}$，所以$b=3a$。因为小正方形EFGH的面积是16，所以$(b−a)^{2}=16$。所以$b−a=4$。所以$a=2$，$b=6$。所以大正方形ABCD的面积$=a^{2}+b^{2}=4+36=40$。

8. [2025成都外国语学校期中]如图,某沿海城市A接到台风预警,在该市正南方向340km的B处有一台风中心,沿BC方向以15km/h的速度移动,已知城市A到BC的距离AD为160km.
(1)台风中心经过多长时间从B点移动到D点?
(2)如果在距台风中心200km的圆形区域内都将受到台风的影响,那么A市受到台风影响的时间为多少小时?

答案：
【解】
(1)由题意可知，$AD⊥BC$，$AB=340km$，$AD=160km$，所以由勾股定理易得$BD=300km$。
因为$300÷15=20(h)$，
所以台风中心经过20h从B点移动到D点。
(2)如图，在射线BC上取点E，F，使得$AE=AF=200km$。又因为$AD⊥BC$，所以$EF=2ED$。
在$Rt△AED$中，由勾股定理易得$ED=120km$，

所以$EF=2ED=240km$。
因为$240÷15=16(h)$，
所以A市受到台风影响的时间为16h。

9. 综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图①是著名的赵爽弦图,由四个全等的直角三角形和一个正方形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于c^2,另一种是等于四个直角三角形与一个小正方形的面积之和,即$\frac{1}{2}ab×4+(b-a)^2,从而得到等式c^2= \frac{1}{2}ab×4+(b-a)^2,$化简便得结论a^2+b^2= c^2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】向常春在2010年构造发现了一个新的证法：把两个全等的直角△ABC和△DEA如图②放置,AB= DE= a,AC= AE= b,BC= AD= c,∠BAC= ∠DEA= 90°,显然BC⊥AD.
(1)连接BD,CD,请用a,b,c分别表示出四边形ABDC,梯形AEDC,△EBD的面积,再探究这三个图形面积之间的关系,验证勾股定理a^2+b^2= c^2.(对角线互相垂直的四边形的面积等于对角线乘积的一半)
【解】(1)$S_{四边形ABDC}=$$\frac {1}{2}c^{2}$，
$S_{梯形AEDC}=$$\frac {1}{2}(b+a)b$，
$S_{△EBD}=$$\frac {1}{2}a(a-b)$。
由图可知$S_{四边形ABDC}=S_{梯形AEDC}+S_{△EBD}$，即$\frac {1}{2}c^{2}=\frac {1}{2}(b+a)b+\frac {1}{2}a(a-b)$，
整理得$b^{2}+a^{2}=c^{2}$。
【方法迁移】请利用“双求法”解决下面的问题：
(2)如图③,在Rt△ABC中,∠ACB= 90°,CD是AB边上的高,AC= 4,BC= 3,求CD的长；
【解】(2)在$Rt△ABC$中，$∠ACB=90^{\circ }$，$AC=4$，$BC=3$，
$AB^{2}=AC^{2}+BC^{2}$，所以$AB=$5。
因为CD是AB边上的高，$∠ACB=90^{\circ }$，
所以$S_{△ABC}=\frac {1}{2}AC\cdot BC=\frac {1}{2}AB\cdot CD$，即$\frac {1}{2}×4×3=\frac {1}{2}×5×CD$，所以$CD=$$\frac {12}{5}$。
(3)如图④,在△ABC中,AD是BC边上的高,AB= 4,AC= 5,BC= 6,求BD的长.
【解】(3)设$BD=$x，则$CD=BC-BD=$$6-x$。
在$Rt△ABD$中，$AD^{2}=AB^{2}-BD^{2}=$$4^{2}-x^{2}$；
在$Rt△ACD$中，$AD^{2}=AC^{2}-CD^{2}=$$5^{2}-(6-x)^{2}$，
所以$4^{2}-x^{2}=5^{2}-(6-x)^{2}$，
解得$x=\frac {9}{4}$，所以$BD=$$\frac {9}{4}$。

答案： 【解】
(1)$S_{四边形ABDC}=\frac {1}{2}AD\cdot BC=\frac {1}{2}c^{2}$，
$S_{梯形AEDC}=\frac {1}{2}(AC+ED)\cdot AE=\frac {1}{2}(b+a)b$，
$S_{△EBD}=\frac {1}{2}ED\cdot BE=\frac {1}{2}a(a-b)$。
由图可知$S_{四边形ABDC}=S_{梯形AEDC}+S_{△EBD}$，即$\frac {1}{2}c^{2}=\frac {1}{2}(b+a)b+\frac {1}{2}a(a-b)$，
整理得$b^{2}+a^{2}=c^{2}$。
(2)在$Rt△ABC$中，$∠ACB=90^{\circ }$，$AC=4$，$BC=3$，
$AB^{2}=AC^{2}+BC^{2}$，所以$AB=5$。
因为CD是AB边上的高，$∠ACB=90^{\circ }$，
所以$S_{△ABC}=\frac {1}{2}AC\cdot BC=\frac {1}{2}AB\cdot CD$，即$\frac {1}{2}×4×3=\frac {1}{2}×5×CD$，所以$CD=\frac {12}{5}$。
(3)设$BD=x$，则$CD=BC-BD=6-x$。
在$Rt△ABD$中，$AD^{2}=AB^{2}-BD^{2}=4^{2}-x^{2}$；
在$Rt△ACD$中，$AD^{2}=AC^{2}-CD^{2}=5^{2}-(6-x)^{2}$，
所以$4^{2}-x^{2}=5^{2}-(6-x)^{2}$，
解得$x=\frac {9}{4}$，所以$BD=\frac {9}{4}$。