《2025年真题圈七年级数学下册北师大版陕西专版》

10. (期中·23 - 24西安铁一中)如图，已知线段AB = 30 m，射线AC⊥AB于点A，射线BD⊥AB于B，M点从B点向A运动，每秒走1 m，N点从B点向D运动，每秒走4 m，M，N同时从B出发，若射线AC上有一点P，使得△PAM和△MBN全等，则线段AP的长度为(　　　)m.

A. 6或60
B. 60
C. 24或60
D. 6

答案： A[解析]根据题意,设运动时间为t s,
所以BM = t m,BN = 4t m
①若点M是AB的中点,
即当AM = BM,AP = BN时,△APM≌△BNM.
因为AB = 30 m,所以AM = BM = $\frac{1}{2}$AB = $\frac{1}{2}$×30 = 15 m,所以t = 15,
所以AP = BN = 4×15 = 60(m).
②若AM＞BM,则当AM = BN,AP = BM时,Rt△AMP≌Rt△BNM,此时BM + BN = 30 m,即t + 4t = 30,解得t = 6,所以AP = BM = 6 m.
③若AM＜BM,因为点N运动的速度大于点M运动的速度,即BN＞BM,所以此情况不存在.
综上所述,线段AP的长度为6 m或60 m.故选A.

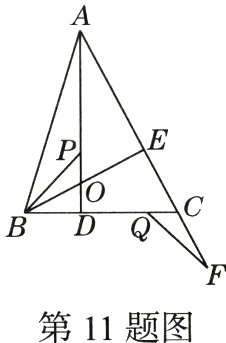
11. (月考·23 - 24西安高新一中创新班改编)如图，在△ABC中，BC = 7，AD⊥BC于D，BE⊥AC于E，AD，BE相交于点O. 若点F是直线AC上的一点，且CF = BO. 动点P从点O出发，沿线段OA以每秒1个单位长度的速度向终点A运动，动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动，P，Q两点同时出发，当点P到达点A时，P，Q两点同时停止运动，设点P的运动时间为t s，则当t的值为________时，以点B，O，P为顶点的三角形与以点F，C，Q为顶点的三角形全等.

答案：
$\frac{7}{5}$或$\frac{7}{3}$[解析]由题意得,OP = t,BQ = 4t,OB = CF,∠BOP = ∠QCF.
①当Q在边BC上时,如图①,△BOP≌△FCQ,
所以OP = CQ,即t = 7 - 4t,t = $\frac{7}{5}$.
②当Q在BC的延长线上时,如图②,△BOP≌△FCQ,
所以OP = CQ,即t = 4t - 7,t = $\frac{7}{3}$.
综上所述,当t为$\frac{7}{5}$或$\frac{7}{3}$时,以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等.
故满足条件的t的值为$\frac{7}{5}$或$\frac{7}{3}$.

12. (期中·22 - 23西安滨河学校)如图，在长方形ABCD中，AB = 6，AD = 8，延长BC到点E，使CE = 2，连接DE，动点P从点B出发，以每秒2个单位长度的速度沿BC→CD→DA向终点A运动，连接AP，设点P的运动时间为t s，当t的值为______________时，△ABP和△DCE全等.

答案： 1或10[解析]①当BP = CE = 2时,△ABP和△DCE全等.
在△ABP和△DCE中,AB = DC,∠ABP = ∠DCE = 90°,BP = CE,△ABP≌△DCE(SAS),
所以BP = 2t = 2,所以t = 1.
②当AP = CE = 2时,△ABP和△DCE全等.
与①同理,根据SAS得△BAP≌△DCE,
所以AP = 22 - 2t = 2,解得t = 10.
所以当t的值为1或10时,△ABP和△DCE全等.
故答案为1或10.

13. 如图，在△ABC中，已知AB = AC，∠BAC = 90°，AH是△ABC的高，AH = 4 cm，BC = 8 cm，直线CM⊥BC，动点D从点C开始沿射线CB方向以3 cm/s的速度运动，动点E也同时从点C开始在直线CM上以1 cm/s的速度向远离C点的方向运动，连接AD，AE，设运动时间为t(t＞0)s.
(1)当t为____________时，△ABD的面积为12 cm²；
(2)当t为____________时，△ABD≌△ACE.

答案：
(1)$\frac{2}{3}$或$\frac{14}{3}$　　
(2)2或4　[解析]
(1)因为$S_{\triangle ABD}$ = $\frac{1}{2}$BD·AH = 12 cm²,AH = 4 cm,所以BD = 6 cm.
若点D在点B的右侧,则CD = BC - BD = 2 cm,t = $\frac{2}{3}$;
若点D在点B的左侧,则CD = BC + BD = 14 cm,t = $\frac{14}{3}$.
综上,当t为$\frac{2}{3}$或$\frac{14}{3}$时,△ABD的面积为12 cm².
(2)①若点E在射线CM上,则点D必在CB上,当BD = CE时,在△ABD和△ACE中,AB = AC,∠ABD = ∠ACE = 45°,BD = CE,所以△ABD≌△ACE(SAS).
此时CE = t cm,BD = (8 - 3t)cm,所以t = 8 - 3t,所以t = 2.
②若点E在CM的反向延长线上,则点D必在CB的延长线上,当BD = CE时,在△ABD和△ACE中,AB = AC,∠ABD = ∠ACE = 135°,BD = CE,所以△ABD≌△ACE(SAS).
此时CE = t cm,BD = (3t - 8)cm,
所以t = 3t - 8,所以t = 4.
综上,当t为2或4时,△ABD≌△ACE
故答案为
(1)$\frac{2}{3}$或$\frac{14}{3}$;
(2)2或4.