第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
26.(期中·22 - 23陕师大附中)(10分)已知直线EF分别交直线AB,CD于点G,H,且∠AGH + ∠DHF = 180°.
(1)如图①,试说明:AB//CD.
(2)如图②,点M,N分别在射线GE,HF上,点P,Q分别在射线GA,HC上,连接MP,NQ,且∠MPG+∠NQH = 90°,分别延长MP,NQ交于点K,试说明:MK⊥NK.
(3)如图③,在(2)的条件下,连接KH,若KH平分∠MKN,且HE平分∠KHD,∠DHG = 5∠MPG,请直接写出∠KMN的度数.
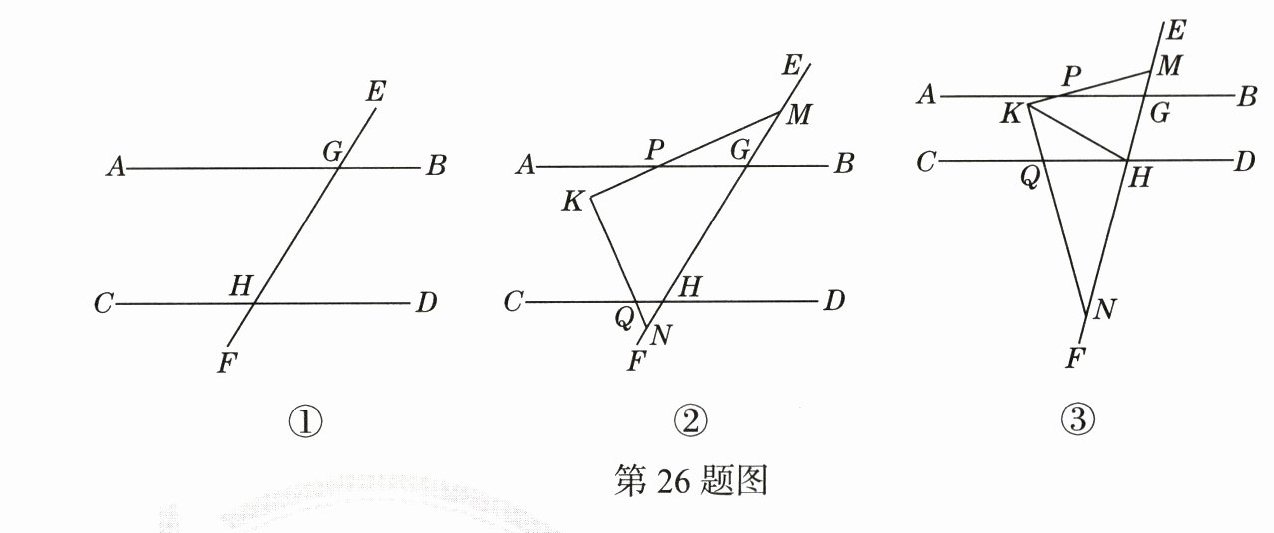
第26题图
(1)如图①,试说明:AB//CD.
(2)如图②,点M,N分别在射线GE,HF上,点P,Q分别在射线GA,HC上,连接MP,NQ,且∠MPG+∠NQH = 90°,分别延长MP,NQ交于点K,试说明:MK⊥NK.
(3)如图③,在(2)的条件下,连接KH,若KH平分∠MKN,且HE平分∠KHD,∠DHG = 5∠MPG,请直接写出∠KMN的度数.

第26题图
答案:
[解]
(1)因为∠AGH + ∠DHF = 180°,∠DHF = ∠EHC,
所以∠AGH + ∠EHC = 180°,所以AB//CD.
(2)如图①,过点K作KO//AB.
由
(1)知AB//CD,所以KO//CD.
因为KO//AB,
所以∠MPG = ∠1.
因为KO//CD,所以∠NQH = ∠2.
因为∠MPG + ∠NQH = 90°,
所以∠1 + ∠2 = 90°,则∠MKN = 90°,即MK⊥NK.

(3)∠KMN = 60°.
分析:如图②,过点M作MT//AB,过点K作KR//AB.
因为AB//CD,所以MT//AB//CD//KR.
因为KH平分∠MKN,∠MKN = 90°,
所以∠MKH = ∠NKH = 45°.
因为∠DHG = 5∠MPG,
所以设∠DHG = 5x,则∠MPG = x.
因为HE平分∠KHD,
所以∠KHM = ∠DHG = 5x,所以∠KHD = 10x,
所以∠KHQ = 180° - 10x.
因为CD//KR,所以∠RKH = ∠KHQ = 180° - 10x.
因为MT//AB//KR,
所以∠TMP = ∠MKR = ∠MPG = x,∠TMH = ∠MHD = 5x.
因为∠MKH = 45°,
所以∠RKH + ∠MKR = 180° - 10x + x = 45°,所以x = 15°.
因为∠KMN = ∠TMH - ∠TMP,
所以∠KMN = 5x - x = 4x = 60°.
[解]
(1)因为∠AGH + ∠DHF = 180°,∠DHF = ∠EHC,
所以∠AGH + ∠EHC = 180°,所以AB//CD.
(2)如图①,过点K作KO//AB.
由
(1)知AB//CD,所以KO//CD.
因为KO//AB,
所以∠MPG = ∠1.
因为KO//CD,所以∠NQH = ∠2.
因为∠MPG + ∠NQH = 90°,
所以∠1 + ∠2 = 90°,则∠MKN = 90°,即MK⊥NK.

(3)∠KMN = 60°.
分析:如图②,过点M作MT//AB,过点K作KR//AB.
因为AB//CD,所以MT//AB//CD//KR.
因为KH平分∠MKN,∠MKN = 90°,
所以∠MKH = ∠NKH = 45°.
因为∠DHG = 5∠MPG,
所以设∠DHG = 5x,则∠MPG = x.
因为HE平分∠KHD,
所以∠KHM = ∠DHG = 5x,所以∠KHD = 10x,
所以∠KHQ = 180° - 10x.
因为CD//KR,所以∠RKH = ∠KHQ = 180° - 10x.
因为MT//AB//KR,
所以∠TMP = ∠MKR = ∠MPG = x,∠TMH = ∠MHD = 5x.
因为∠MKH = 45°,
所以∠RKH + ∠MKR = 180° - 10x + x = 45°,所以x = 15°.
因为∠KMN = ∠TMH - ∠TMP,
所以∠KMN = 5x - x = 4x = 60°.
查看更多完整答案,请扫码查看


