《2025年真题圈七年级数学下册北师大版陕西专版》

25.(月考·23 - 24陕师大附中)(8分)我们知道,通过几何图形的面积可以表示一些代数恒等式.
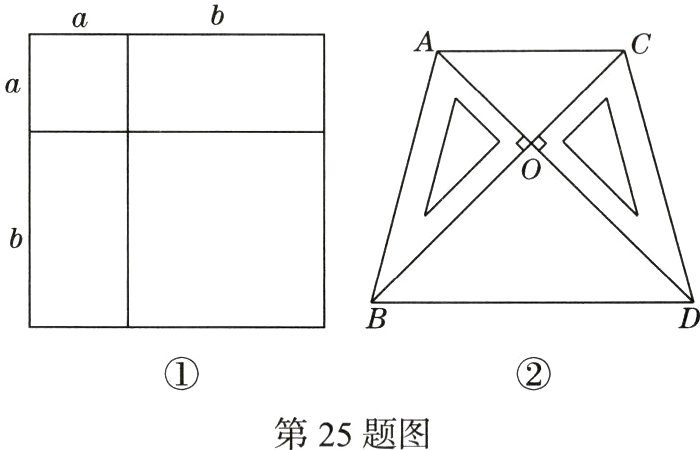
例如图①得到$(a + b)^2 = a^2 + 2ab + b^2,$基于此,请回答下列问题:
直接应用:(1)若$x + y = 3,x^2 + y^2 = 5,$则xy = ________.
类比应用:(2)若x(3 - x) = 1,则$x^2+(x - 3)^2 = ________.$
知识迁移:(3)两块完全一样的直角三角板(∠AOB = ∠COD = 90°)如图②放置,其中A,O,D在一条直线上,连接AC,BD. 若$AD = 16,S_△AOC+S_△BOD = 68,$求一块直角三角板的面积.
　　　　　　　　　　　　　　　　　　　　　　

答案： [解]
(1)2
分析:由(a+b)²=a²+2ab+b²,可得(x+y)²=x²+2xy+y²,因为x+y=3,x²+y²=5,所以xy=(x+y)²−2(x²+y²):=$\frac{3²−5}{2}$=2.
(2)7
分析:因为(a+b)²=a²+2ab+b²,所以[x+(3−x)]²=x²+2x(3−x)+(3−x)²,因为x(3−x)=1,所以x²+(3−x)²=[x+(3−x)]²−2x(3−x)=9−2=7,所以x²+(x−3)²=x²+(3−x)²=7.
(3)设直角三角板的短直角边长为x,，长直角边长为y,即OA=OC=x,OB=OD=y 因为∠AOB=∠COD=90°,且A,O,D在一条直线上,所以∠AOC=∠BOD=90°.因为AD=16,S△Aoc+S△BOD=68,即OA+OD=x+y=16,所以$\frac{1}{2}$OA.OC+$\frac{1}{2}$OB.OD=$\frac{1}{2}$x²+$\frac{1}{2}$y²=68,所以x²+y²=136,所以直角三角板的面积为$\frac{1}{2}$OA.OB=$\frac{1}{2}$xy =$\frac{1}{2}$x(x+y)²−2(x²+y²),=$\frac{1}{2}$x$\frac{16²−136}{2}$,=30.故一块直角三角板的面积为30.