《2025年真题圈七年级数学下册北师大版陕西专版》

8.(期末·23 - 24西安爱知中学)如图,在△ABC中,BD是AC边上的高,∠AEB = 90°,BC = AF,则下列结论正确的有(　　　)
①∠FAD = ∠CBD；②∠ACF = 45°；③CF⊥AB；④△ABF,△CBF的面积分别表示为$S_{△ABF},S_{△CBF},$则$S_{△ABF}:S_{△CBF}= BD:DF；$⑤∠FCB = ∠BAF.
　
A. ①②③　　　　　　　　　
　B. ①③④
C. ①②④⑤　　　　　　　　
　D. ①②③④⑤

答案： D[解析]因为∠AEB=90°,所以∠AEC=90°.因为BD是AC边上的高，所以BD⊥AC于点D,所以∠ADF=∠BDC=90°.因为∠FAD+∠ACB=90°,∠CBD+∠ACB=90°,所以∠FAD=∠CBD,故①正确.在△FAD和△CBD中,∠FAD=∠CBD,∠ADF=∠BDC,AF=BC,所以△FAD≌△CBD(AAS),所以DF=DC,AD=BD,∠AFD=∠BCD,所以∠ACF=∠DFC=45°,∠DAB=∠DBA=45°,故②正确.延长CF交AB于点G,如图因为∠AGC=180°−(∠DAB+∠ACF)=180°−45°−45°=90°,所以CF⊥AB,故③正确,因为AD⊥BF,DC⊥BF,
所以$S_{\triangle ABF}=\frac{1}{2}BF\cdot AD=\frac{1}{2}BF\cdot BD$,$S_{\triangle CBF}=\frac{1}{2}BF\cdot DC=\frac{1}{2}BF\cdot DF$,所以$\frac{S_{\triangle ABF}}{S_{\triangle CBF}}=\frac{\frac{1}{2}BF\cdot BD}{\frac{1}{2}BF\cdot DF}=\frac{BD}{DF}$,即$S_{\triangle ABF}:S_{\triangle CBF}=BD:DF$,故④正确;因为∠BCD=∠AFD,所以∠BCD−45°=∠AFD−45°.因为∠FCB=∠BCD−∠ACF=∠BCD−45°,∠BAF=∠BAD−∠FAD=45°−(90°−∠AFD)=∠AFD−45°,所以∠FCB=∠BAF,故⑤正确,故选D.

9.(期中·22 - 23西安滨河学校)如图所示,(1)在△ABC中,BC边上的高是________；(2)在△AEC中,AE边上的高是________.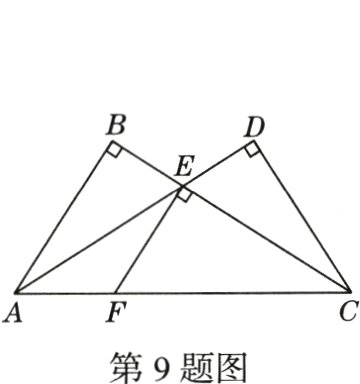

答案：
(1)AB
(2)CD

10.(期末·22 - 23西安交大附中)已知等腰三角形的底边长为8,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长3,那么这个三角形的腰长为________.

答案： 11或5[解析]如图,△ABC为等腰三角形,AB=AC,AH=CH,BC=8.设AH=CH=x,则AB=AC=2x.当AB+AH−(BC+CH)=3时,
2x+x−(x+8)=3,解得x=5.5,所以AB=AC=11.当BC+CH−(AB+AH)=3时,8+x−(2x+x)=3,解得x=2.5,所以AB=AC=5.故答案为11或5.

11.(期末·23 - 24西安曲江一中)如图,AD是△ABC的高,DE是△ABD的中线,BF是△BDE的角平分线.若AD = BD,则∠BFD的度数为________.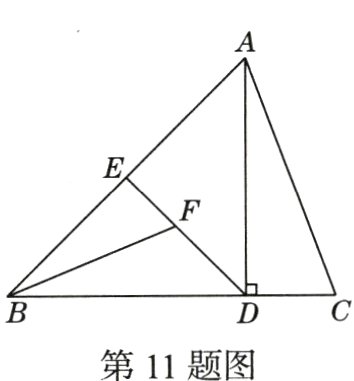

答案： 112.5°[解析]因为AD是△ABC的高，所以∠ADB=90°.因为AD=BD,DE是△ABD的中线，所以∠DAB=∠DBA=45°,DE⊥AB,即∠BED=90°.因为BF是△BDE的角平分线，所以∠EBF=$\frac{1}{2}$∠EBD=22.5°,所以∠EFB=180°−90°−22.5°=67.5°,所以∠BFD=180°−∠EFB=180°−67.5°=112.5°.故答案为112.5°.

12.(期中·22 - 23西安高新一中)如图,在△ABC中,点D是BC的中点,连接AD,点E在AD上,且AE = $\frac{1}{3}$DE,EF⊥BD于点F.若BC = 10,EF = 3,则△ABC的面积为________.
　　

答案： 20[解析]连接BE,如图.因为BC=10,点D是BC的中点,所以BD=DC=$\frac{1}{2}$BC=5.
因为EF⊥BC,且EF=3,所以$S_{\triangle BDE}=\frac{1}{2}BD\cdot EF=\frac{1}{2}\times5\times3=\frac{15}{2}$.又因为AE=$\frac{1}{3}$DE,所以$S_{\triangle ABE}=\frac{1}{3}S_{\triangle BDE}=\frac{1}{3}\times\frac{15}{2}=\frac{5}{2}$,所以$S_{\triangle ABD}=S_{\triangle ADC}=S_{\triangle BDE}+S_{\triangle ABE}=\frac{15}{2}+\frac{5}{2}=10$,所以$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ADC}=2\times10=20$.故答案为20.

13.(期末·23 - 24陕师大附中)如图,已知△ABC的面积为36,点D,E分别在边BC,AC上,且BD = CD,CE = 2AE,AD与BE相交于点F.若△AEF的面积为3,则图中阴影部分的面积为________.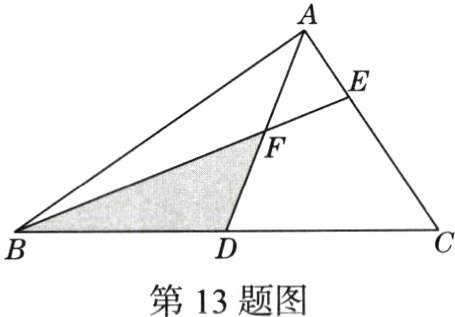

答案： 9[解析]连接CF,如图所示,因为△AEF的边AE与△CEF的边CE上的高相同,CE=2AE,
所以$S_{\triangle CEF}=2S_{\triangle AEF}=2\times3=6$.又因为$S_{\triangle ABC}=36,BD =CD$,所以$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}=18$,所以$S_{\triangle CFD}=18−3−6=9$.因为△BFD与△CFD等底同高，所以$S_{\triangle BFD}=S_{\triangle CFD}=9$,即阴影部分面积为9.故答案为9.

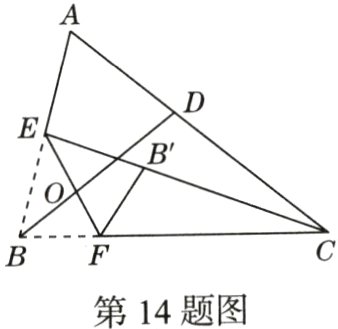
14.(期中·22 - 23西工大附中)在如图所示的△ABC纸片中,点E是边AB的中点,点F是边BC上任意一点,现将△BEF沿EF折叠,得到△B'EF,折痕EF与△ABC的角平分线BD相交于点O,连接CB',当线段EB'与CB'的长度和最小时,∠EOB = 100°,则此时∠B'CB = ______°.

答案： 20[解析]当E,B',C三点共线时,线段EB'与CB'的长度和最小,设CE,BD交于点P,如图.因为BD平分∠ABC,所以∠ABD=∠CBD.设∠ABD=∠CBD=α,
因为∠EOB=100°,所以∠BEO=∠B'EO=80°−α,所以∠BEB'=2(80°−α)=160°−2α,所以∠EPB=180°−∠BEB'−∠EBO=180°−160°+2α−α=20°+α,∠BPC=180°−∠EPB=180°−20°−α=160°−α,所以∠B'CB=180°−∠BPC−∠CBD=180°−(160°−α)−α=20°.故答案为20.