《2025年真题圈七年级数学下册北师大版陕西专版》

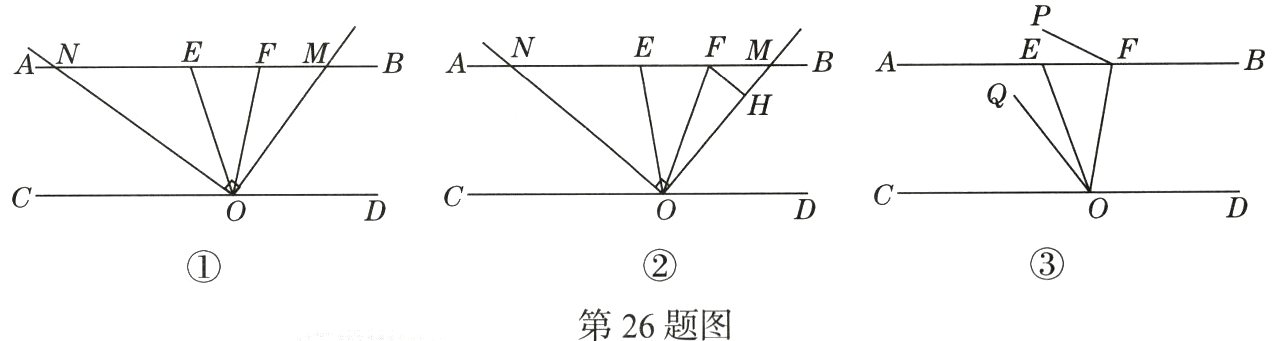
26.(月考·23 - 24陕师大附中)(10分)如图,已知$AB// CD$,O为直线CD上一点,动点E,F在直线AB上(F在E的右侧)且满足$\angle EOF = 30^{\circ}$,$OM$在∠EOF外部且OM平分∠EOD,$ON\perp OM$交AB于点N.
(1)如图①,若$\angle FOM = 24^{\circ}$,求∠ENO的度数.
(2)如图②,若射线OM上有一点H满足$\angle MFH = 2\angle FOH$,请探究∠FHO与∠ENO之间的数量关系并说明理由.
(3)如图③,若$\angle FEO = 70^{\circ}$,射线FP从与射线FE重合的位置出发,绕点F以每秒$5^{\circ}$的速度顺时针旋转,同时射线OQ从与射线OE重合的位置出发,绕点O以每秒$3^{\circ}$的速度逆时针旋转,设旋转的时间为t s($0\leq t\leq72$),当射线FP和射线OQ平行时,求出t的值.

答案：
(1)因为∠EOF=30°,∠FOM=24°,
所以∠EOM=∠EOF+∠FOM=54°.
因为OM平分∠EOD,所以∠EOM=∠DOM=54°.
因为ON⊥OM,所以∠MON=90°,
所以∠CON=180°−∠MON−∠DOM=36°.
因为AB//CD,所以∠ENO=∠CON=36°.
(2)∠FHO与∠ENO之间的数量关系为∠FHO+3∠ENO=210°.理由如下:
设∠FOH=x,则∠MFH=2∠FOH=2x.
因为∠EOF=30°,∠FOH=x,
所以∠EOM=∠EOF+∠FOH=30°+x.
因为OM平分∠EOD,所以∠EOM=∠DOM=30°+x.
因为ON⊥OM,所以∠MON=90°,
所以∠CON=180°−∠MON−∠DOM=60°−x.
因为AB//CD,
所以∠ENO=∠CON=60°−x,∠FMH=∠DOM=30°+x.因为∠FHO=180°−∠MHF=∠MFH+∠FMH=30°+3x,∠ENO=∠CON=60°−x,
所以∠FHO+3∠ENO=210°.
(3)因为∠FEO=70°,∠EOF=30°,AB//CD,
所以∠EFO=80°,∠EOC=70°,
所以∠EFO+∠EOF=110°.
分情况讨论:当0≤t≤36时,
①如图①,当∠PFO+∠FOQ=180°时,FP//OQ,
所以∠EFP+∠EOQ=8t°=180°−110°=70°,
解得t=$\frac{70}{8}$=$\frac{35}{4}$.
②如图②,当∠PFO=∠FOQ时,FP//OQ,
因为∠EFO=80°,∠EOF=30°,
所以∠BFO=100°,
所以∠PFO=100°+180°−5t°,∠FOQ=3t°+30°,
所以100°+180°−5t°=3t°+30°,
解得t=$\frac{250}{8}$=$\frac{125}{4}$.
当36＜t≤72时,
③如图③,当∠PFO+∠FOQ=180°时,FP//OQ.
因为∠EFO=80°,∠EOF=30°,
所以∠PFO=(360°−5t°)−80°=280°−5t°,∠FOQ=360°−30°−3t°=330°−3t°,
所以280°−5t°+330°−3t°=180°,解得t=$\frac{430}{8}$=$\frac{215}{4}$.
④如图④,当∠PFO=∠FOQ时,FP//OQ.
因为∠EFO=80°,∠EOF=30°,
所以∠PFO=80°−(360°−5t°)=5t°−280°,
∠FOQ=(360°−3t°)−30°=330°−3t°,
所以5t°−280°=330°−3t°,
解得t=$\frac{610}{8}$=$\frac{305}{4}$＞72,舍去.
综上所述，当t=$\frac{35}{4}$或t=$\frac{125}{4}$或t=$\frac{215}{4}$时，射线FP和射线OQ平行.