《2025年真题圈七年级数学下册北师大版陕西专版》

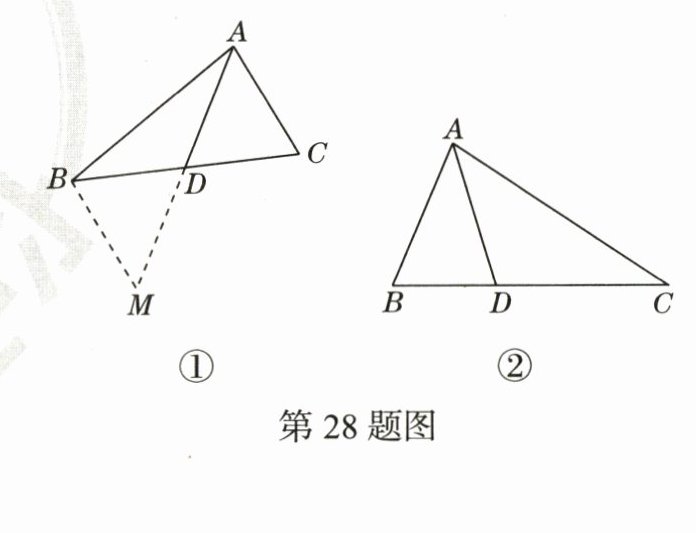
28.(期末·22 - 23西安交大附中)在本学期的数学学习中,老师提出了这样一个问题:
如图①,在△ABC中,AB = 10,AC = 6,D是BC的中点,求BC边上的中线AD的取值范围.
阅读理解:
小明在班内经过合作交流,得到了如下的解决方法:
(1)如图①,延长AD到点M,使AD = DM,连接BM,根据________可以判定△ADC≌△MDB,得出AC = BM,这样就能把线段AB,AC,2AD集中在△ABM中,利用三角形三边的关系,即可得出中线AD的取值范围.
方法感悟:
我们发现,几何图形中出现能表示相等数量关系的条件时,如:"中点""角平分线"等,往往可以考虑作辅助线,构造全等三角形,从而达到解决问题的目的.
问题解决:
(2)如图②,在△ABC中,∠B = 2∠C,∠BAC的平分线AD交BC边于点D,若AB = 3,BD = 2,求AC的长.

答案：
(1)SAS
分析:因为D是BC的中点，所以BD=CD.在△ADC和△MDB中,CD=BD,∠ADC=∠MDB,AD=MD,所以△ADC≌△MDB(SAS).
(2)延长AB到点P,使BP=BD,连接DP,如图,则∠P=∠BDP.因为∠ABD+∠PBD=180°,∠PBD+∠P+∠BDP=180°,所以∠ABD=∠P+∠BDP=2∠P,BP=BD=2,所以AP=AB+BP=5.因为∠ABC=2∠C,所以∠P=∠C.因为AD为∠BAC的平分线,所以∠BAD=∠CAD.又因为AD=AD,所以△ADP≌△ADC(AAS),所以AC=AP=5.