《2025年真题圈七年级数学下册北师大版陕西专版》

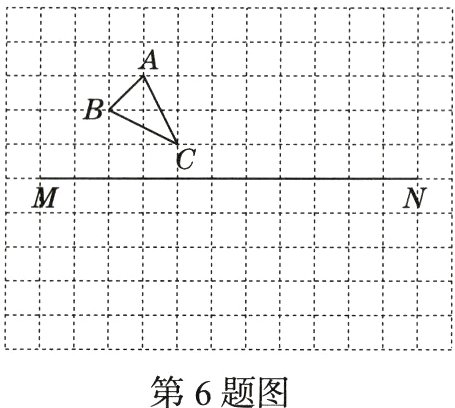
6.(期末·23 - 24西安尊德中学)如图,已知△ABC的三个顶点在格点上.
　　(1)画出△A₁B₁C₁,使它与△ABC关于直线MN对称.
　　(2)在直线MN上找出一点D，使得∠BDM = ∠CDN,并说明理由.
　　　　　　　　　　　　　　　

答案：
[解]
(1)如图，$\triangle A_{1}B_{1}C_{1}$即所求

(2)如图，点D即所求. 理由:由轴对称的性质可知，$∠CDN = ∠C_{1}DN$，因为$∠BDM = ∠C_{1}DN$，所以$∠BDM = ∠CDN$.

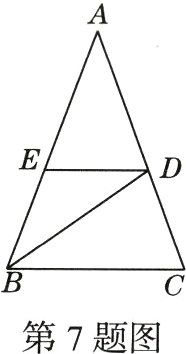
7.(期中·22 - 23西安交大附中)如图,在等腰三角形ABC中,AB = AC,∠A = 40°,BD是△ABC的角平分线,DE//BC,则∠BDE的度数为(　　　)
　　A.20°　　　　　B.35°　　　　　C.40°　　　　　D.70°
　　　　　

答案： B　[解析]因为$AB = AC$，所以$∠ABC = ∠C$. 因为$∠A = 40^{\circ}$，所以$∠ABC=\frac{1}{2}×(180^{\circ}-40^{\circ}) = 70^{\circ}$. 因为BD是$\triangle ABC$的角平分线，所以$∠DBC=\frac{1}{2}∠ABC = 35^{\circ}$. 因为$DE// BC$，所以$∠BDE = ∠DBC = 35^{\circ}$. 故选B.

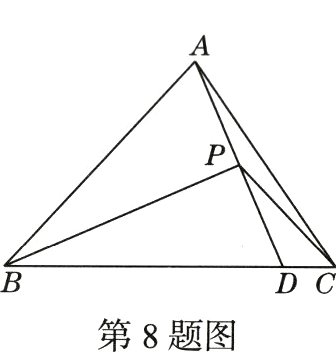
8.(期末·23 - 24西安爱知中学)如图,在△ABC中,点D为BC边上的一点,且BD = BA,连接AD,BP平分∠ABC交AD于点P,连接PC,若△ABC的面积为6cm²,则△BPC的面积为(　　　)
　　A.3cm²　　　　B.4cm²　　　　C.$\frac{7}{2}$cm²　　　　D.$\frac{16}{5}$cm²
　　　　　

答案： A[解析]因为$BD = BA$，BP平分$∠ABC$，所以$AP = PD$，所以$S_{\triangle APB}=S_{\triangle DPB}$，$S_{\triangle APC}=S_{\triangle DPC}$，所以$S_{\triangle BPC}=\frac{1}{2}×S_{\triangle ABC}=3(cm^{2})$. 故选A.

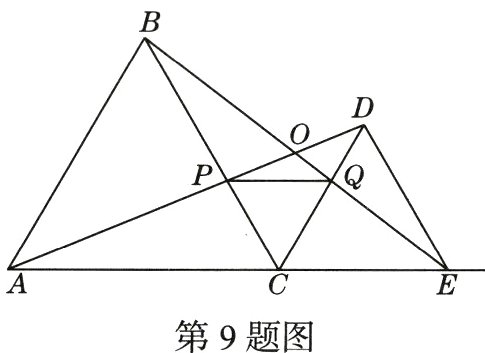
9.(期末·23 - 24西安尊德中学)如图,A,C,E三点在同一直线上,△ABC和△DCE都是等边三角形，连接AD,BE，分别交BC,CD于点P,Q,AD与BE相交于点O,连接PQ,下列结论正确的有(　　　)
　　①△ACD≌△BCE;②CP = CQ;③∠AOE = 120°;④PQ//AE;⑤DP = DE.
　　A.2个　　　　B.3个　　　　　C.4个　　　　　D.5个
　　　　　

答案： C[解析]因为$\triangle ABC$和$\triangle DCE$都是等边三角形，所以$AC = BC$，$∠ACB = 60^{\circ}$，$CD = CE = DE$，$∠DCE = 60^{\circ}$，所以$∠BCD = 180^{\circ}-∠ACB - ∠DCE = 60^{\circ}$，所以$∠ACD = ∠ACB+∠BCD = 120^{\circ}$，$∠BCE = ∠BCD+∠DCE = 120^{\circ}$，所以$∠ACD = ∠BCE$，所以$\triangle ACD\cong\triangle BCE(SAS)$，①正确；因为$\triangle ACD\cong\triangle BCE$，所以$∠CAP = ∠CBQ$. 因为$∠ACB = 60^{\circ}$，$∠BCD = 60^{\circ}$，所以$∠ACB = ∠BCD$. 因为$AC = BC$，所以$\triangle ACP\cong\triangle BCQ(ASA)$，所以$CP = CQ$，②正确；因为$∠CBQ+∠BOP = ∠CAP+∠ACB$，$∠CAP = ∠CBQ$，所以$∠BOP = ∠ACB = 60^{\circ}$，所以$∠AOE = 180^{\circ}-∠BOP = 120^{\circ}$，③正确；因为$CP = CQ$，$∠BCD = 60^{\circ}$，所以$∠CPQ = 60^{\circ}$，所以$∠CPQ = ∠ACB = 60^{\circ}$，所以$PQ// AE$，④正确；因为$DE = CD$，由图易知$DC＞PC$，所以$DE＞DP$，⑤不正确，综上，正确的结论是①②③④，共4个. 故选C.

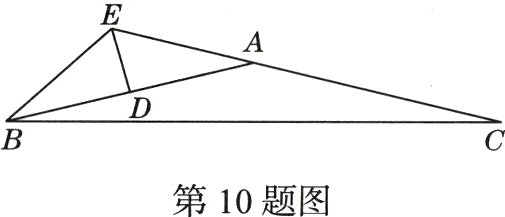
10.(期末·22 - 23西安爱知中学)如图,在一张纸片上将△BED翻折得到△AED,并以AB为边作等腰△ABC,其中AB = AC,且E,A,C三点共线，∠EBC = 42°,则∠BAC的度数是__________.
　　　　　

答案： $152^{\circ}$[解析]由折叠可知$EA = EB$，所以$∠EBA = ∠EAB$. 因为$AB = AC$，所以$∠ABC = ∠C$. 因为$∠EAB+∠BAC = 180^{\circ}$，$∠ABC + ∠C+∠BAC = 180^{\circ}$，所以$∠EAB = ∠ABC + ∠C$，所以$∠EBC = ∠EBA+∠ABC = ∠EAB+∠ABC = 3∠ABC = 42^{\circ}$，所以$∠ABC = 14^{\circ}$，所以$∠BAC = 180^{\circ}-2×14^{\circ}= 152^{\circ}$. 故答案为$152^{\circ}$.