《2025年真题圈七年级数学下册北师大版陕西专版》

19.(月考·23 - 24西工大附中改编)如图,在△ABC中,AC = BC = 10,AB = 12,△ABC的面积为48.P为AB上一动点,点Q在AC上,在点P运动的过程中,当△AQP≌△BPC时,△CPQ的面积为(　　　)


A.52　　　　
　B.32　　　　　
　C.40　　　　　
　D.24

答案： B[解析]因为△AQP≌△BPC,所以AP=BC=10,AQ=BP.因为AB=12,所以AQ=BP=2,所以CQ=AC−AQ=8.过点C作CD⊥AB于点D,过点P作PH⊥AC于点H,如图
$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD = 48$,解得CD=8,所以$S_{\triangle APC}=\frac{1}{2}AP\cdot CD=\frac{1}{2}AC\cdot PH$,所以10×8 = 10PH,所以PH=8,所以$S_{\triangle CPQ}=\frac{1}{2}CQ\cdot PH=\frac{1}{2}\times8\times8 = 32$.故选B.

20.(期末·22 - 23西安高新一中)如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD = CA；连接BC并延长到E,使CE = CB.小明认为只要知道DE的长度,就知道AB的长度,小明是根据△ABC≌△DEC来判定DE = AB的,那么判定这两个三角形全等的基本事实或定理是(　　　)
A. SSS　　　
　B. SAS　　　
　C. ASA　　　
　D. AAS

答案： B[解析]由题意知CD=CA,CE=CB,在△DEC和△ABC中,CD=CA,∠DCE=∠ACB,CE=CB,所以△DEC≌△ABC(SAS).故选B.

21.(期末·22 - 23西安爱知中学)如图,点E在△ABC外部,点D在△ABC的BC边上,DE交AC于点F,若∠1 = ∠2 = ∠3,AE = AC,则(　　　)


A. △ABD≌△AFE　　　　　　　　　
　B. △AFE≌△ADC
C. △AFE≌△DFC　　　　　　　　　
　D. △ABC≌△ADE

答案： D[解析]因为∠1=∠2=∠3,所以∠1+∠DAC=∠2+∠DAC,所以∠BAC=∠DAE.因为∠ADC+∠ADB=180°,∠ADB+∠1+∠B=180°,所以∠ADC=∠B+∠1,所以∠ADE+∠3=∠B+∠1,所以∠B=∠ADE.在△ABC和△ADE中,∠B=∠ADE,∠BAC=∠DAE,AC=AE,所以△ABC≌△ADE(AAS).故选D.

22.(期末·22 - 23西安铁一中)如图,AC,BD相交于点O,AB = DC,添加一个条件,不能证明OB = OC的是(　　　)


A. ∠B = ∠C
　B. ∠A = ∠D　
　C. AC = BD　
　D. OA = OD

答案： D[解析]A.因为AB=DC,∠AOB=∠DOC,所以添加条件∠B=∠C,利用AAS可以证明△AOB≌△DOC,所以OB =OC.
B.因为AB=DC,∠AOB=∠DOC,所以添加条件∠A=∠D,利用AAS可以证明△AOB≌△DOC,所以OB=OC.
C.连接AD,如图所示.因为AB=DC,AD=AD,所以添加条件AC=BD,利用SSS 可以证明△ABD≌△DCA,所以∠B=∠C.因为∠AOB=∠COD,
所以△AOB≌△DOC,所以OB=OC.
D.因为AB=DC,∠AOB=∠DOC,所以添加条件OA=OD,用SSA不能证明△AOB≌△DOC,所以无法证明OB=OC.故选D.

23.(期中·22 - 23西安滨河学校)如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带________去玻璃店(填序号).
　　　　

答案： ③[解析]③不仅保留了原来三角形的两个角还保留了一条边，可以根据ASA来配一块一样的玻璃,故答案为③.

24.(期末·23 - 24西安高新三初)如图是正方形网格,点A,B,C,D均落在格点上,则∠DCB + ∠ACB的度数为________.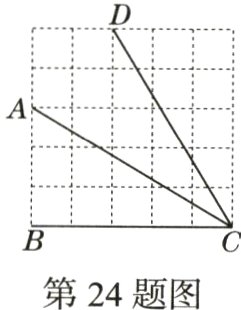

答案： 90°[解析]如图,根据题意，得AB=DE,BC=EC,∠B=∠E =90°.所以△ABC≌△DEC(SAS),所以∠ACB=∠DCE,
所以∠DCB+∠ACB =∠DCB+∠DCE=∠BCE =90°.故答案为90°.