《2025年真题圈七年级数学下册北师大版陕西专版》

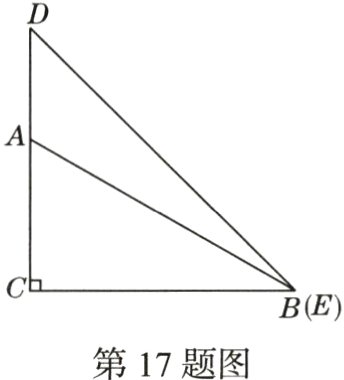
17.(期中·23 - 24西安爱知中学改编)小明将两个直角三角形的直角顶点重合后按如图所示摆放,其中∠ACB = ∠DCE = 90°, ∠BAC = 60°,∠ABC = 30°,∠DEC = ∠CDE = 45°(此时点B与点E重合).他固定三角形DCE,将三角形ACB绕点C顺时针以每秒6°的速度旋转,设它的旋转时间为t s(0 ≤ t ≤ 60),则在旋转过程中,当边AB//DE时,t =______.
　　　

答案：
2.5或32.5　[解析]如图①,延长CA交DE于点F,
因为AB//DE,∠CAB = 60°,
所以∠CFE =∠CAB = 60°,
所以∠CFD = 180° - 60° = 120°.
又∠D +∠DCF +∠CFD = 180°,∠D = 45°,
所以∠DCF = 180° - 120° - 45° = 15°,
所以三角形ACB旋转的角度为15°,
所以t = 15÷6 = 2.5;


如图②,延长AC交DE于点F,同理可得∠DCF = 15°,
所以三角形ACB旋转的角度为180° + 15° = 195°,
所以t = 195÷6 = 32.5.
故答案为2.5或32.5.

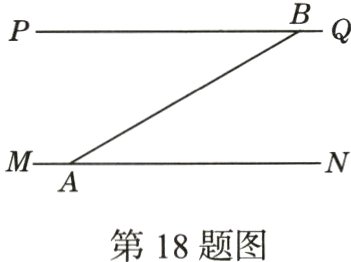
18.(期中·22 - 23西安高新一中)汉江是长江的最大支流,在历史上占据重要地位,常与长江、淮河、黄河并列,合称“江淮河汉”.每年汛期来临之时,汉江防汛抗旱指挥部都会在一危险地带两岸各安置一组探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射出的光线自AM顺时针旋转至AN便立即回转,灯B射出的光线自BQ顺时针旋转至BP便立即回转,两灯不停交叉照射巡视,已知灯A转动的速度是3°/s,灯B转动的速度是1°/s,假定这一带汉江两岸河堤是平行的,即PQ//MN,且∠BAN = 30°,转动时间是t s.
(1)当t =______时,灯A射出的光线第一次平分∠BAM,此时灯A射出的光线记为射线AT,当t =______时,灯A射出的光线AC第一次与射线AT垂直.
(2)若两灯同时转动,t = 90时,两束光线所在直线的位置关系是______.(填“平行”或“垂直”)
(3)若灯B射出的光线先转动30 s,灯A射出的光线才开始转动,在灯B射出的光线到达BP之前,灯A转动几秒,两灯射出的光线互相平行.
　　　　　　　　　　　　　　　　　　　

答案：
[解]
(1)25 55　分析:如图①,因为∠BAN = 30°,
所以∠BAM = 180° - 30° = 150°.
因为AT平分∠BAM,所以∠MAT = $\frac{1}{2}$∠BAM = 75°,
所以此时灯A转动时间为75÷3 = 25(s).
因为AC⊥AT;所以∠TAC = 90°,所以∠MAC = 75° + 90° = 165°,所以此时灯A的转动时间为165÷3 = 55(s).
(2)平行　分析:两灯同时转动，当t = 90时,灯A转动的角度为90×3° = 270°,灯B转动的角度为90×1° = 90°.
因为270° - 180° = 90°,所以此时灯A发出的光线AC⊥MN,灯B发出的光线BD⊥PQ,如图②,
所以∠CAN =∠DBP = 90°.
因为PQ//MN,所以∠CEB =∠CAN = 90°,
所以∠CEB =∠DBP = 90°,所以AC//BD,
即t = 90时，两束光线所在直线的位置关系是平行.

(3)设灯A转动x s后，两灯射出的光线互相平行.
①当0 ＜ x ≤ 60时,根据题意,得3x =(30 + x)×1,
解得x = 15;
②当60 ＜ x ≤ 120时，
根据题意得3x - 180+(30 + x)×1 = 180,解得x = 82.5;
③当120 ＜ x ≤ 150时,根据题意得3x - 180×2=(x + 30)×1,解得x = 195 ＞ 150(不合题意).
综上可知，当A灯转动15 s或82.5 s时，两灯射出的光线互相平行.