《2025年真题圈七年级数学下册北师大版陕西专版》

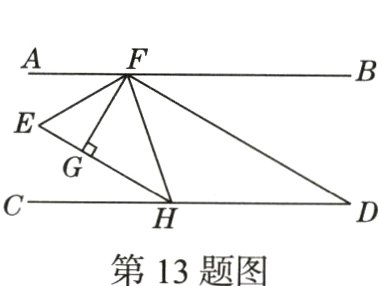
13.如图,AB//CD,F为AB上一点,FD//EH,过点F作FG⊥EH于点G,FE平分∠AFG,且∠AFG = 2∠D,则下列结论:
①∠D = 40°;
②2∠D + ∠EHC = 90°;
③FD平分∠HFB;
④FH平分∠GFD.
其中正确结论的个数是(　　　　)
　
A. 1 B. 2 C. 3 D. 4
　　　

答案： A　[解析]因为AB//CD,所以∠BFD =∠D.
因为FG⊥EH,所以∠FGH = 90°.
因为FD//EH,所以∠EHC =∠D,∠DFG +∠FGH = 180°,所以∠DFG = 90°.
因为∠AFG = 2∠D,
所以∠AFG +∠GFD +∠BFD = 3∠D + 90° = 180°,
所以∠D = 30°,所以∠EHC =∠D = 30°,
所以2∠D +∠EHC = 90°.故①错误,②正确.
因为∠GFH的角度不确定,∠GFD = 90°,∠BFD = 30°,
所以∠HFD不一定为30°或45°,则FD不一定平分∠HFB,FH 不一定平分∠GFD.故③④均不一定正确.故选A.

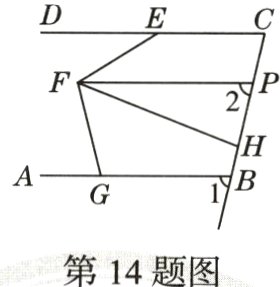
14.(月考·22 - 23西安行知中学)如图,已知DC//FP,∠1 = ∠2,∠FED = 32°,∠AGF = 76°,FH平分∠EFG,则∠PFH =______.
　　　

答案： 22°　[解析]因为∠1 =∠2,所以PF//AB,
所以∠PFG =∠AGF = 76°.
因为DC//FP,所以∠EFP =∠FED = 32°,
所以∠EFG =∠EFP +∠PFG = 108°.
因为FH平分∠EFG,所以∠HFG = $\frac{1}{2}$∠EFG = 54°,
所以∠PFH =∠PFG -∠HFG = 22°.故答案为22°.

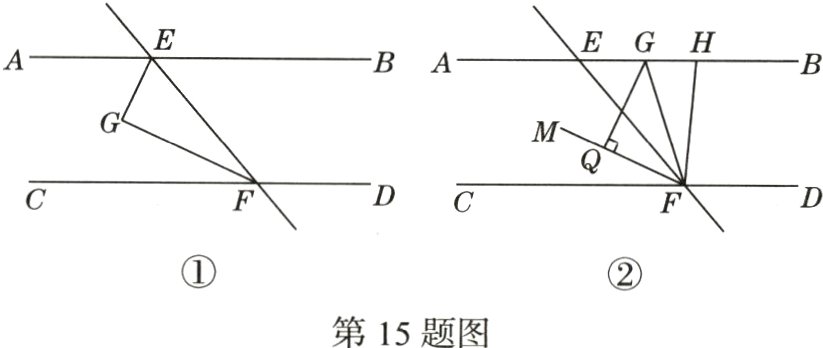
15.(月考·23 - 24西安铁一中改编)已知:直线AB//CD,直线EF与直线AB,CD分别相交于点E,F.
(1)如图①,若EG平分∠AEF,FG平分∠EFC,则直线EG与FG的位置关系是______.
(2)如图②,若点H是射线EB上一动点,FG平分∠EFH,FM平分∠EFC,过点G作GQ⊥FM于点Q,则∠EHF与∠FGQ的关系是______.
　　　

答案：

(1)EG⊥FG　
(2)∠EHF = 2∠FGQ　[解析]
(1)如图,过点G作GM//AB,因为AB//CD,
所以AB//GM//CD,
所以∠EGM =∠AEG,∠FGM =∠GFC.
因为EG平分∠AEF,FG平分∠EFC,
所以∠AEG = $\frac{1}{2}$∠AEF,∠GFC = $\frac{1}{2}$∠EFC,
所以∠EGF =∠EGM +∠FGM =∠AEG +∠GFC = $\frac{1}{2}$(∠AEF +∠EFC)= 90°,
所以EG⊥FG.
(2)因为AB//CD,
所以∠EHF +∠CFH = 180°,∠BGF =∠CFG,
所以∠EHF = 180° -∠CFH.
因为FG平分∠EFH,FM平分∠EFC,
所以∠EFG = $\frac{1}{2}$∠EFH、∠CFM =∠EFM = $\frac{1}{2}$∠EFC,
所以∠BGF =∠CFG =∠CFE + $\frac{1}{2}$∠EFH.
因为GQ⊥FM，
所以∠GQF = 90°
因为AB//CD,同
(1)可得∠GQF =∠AGQ +∠CFQ = 90°,所以∠AGQ = 90° -∠CFQ = 90° - $\frac{1}{2}$∠CFE.
所以∠FGQ = 180° -∠AGQ -∠BGF = 180° - (90° - $\frac{1}{2}$∠CFE) - (∠CFE + $\frac{1}{2}$∠EFH)= 90° - $\frac{1}{2}$(∠EFH +∠CFE)= 90° - $\frac{1}{2}$∠CFH.
因为∠EHF = 180° -∠CFH = 2(90° - $\frac{1}{2}$∠CFH),
所以∠EHF = 2∠FGQ.
故答案为
(1)EG⊥FG;
(2)∠EHF = 2∠FGQ.

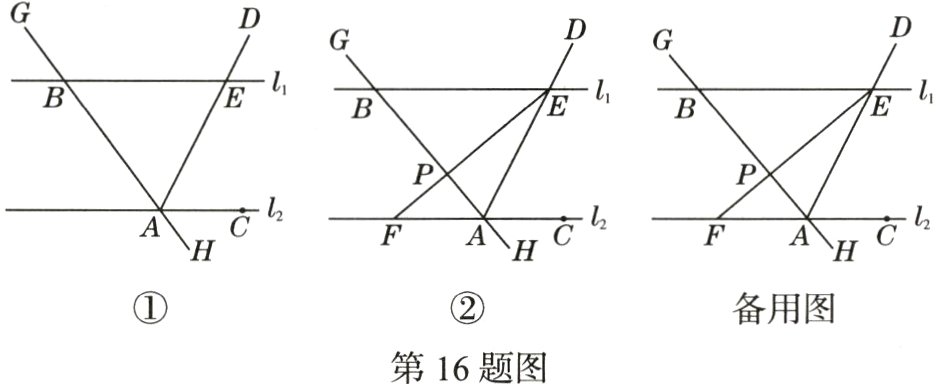
16.(月考·22 - 23西安滨河学校)如图①,已知直线GH与直线l₁,l₂分别交于B,A两点,点C在直线l₂上,射线AD平分∠BAC,交直线l₁于点E,∠GBE = 2∠BAE.
(1)请直接写出直线l₁与l₂的位置关系是____________________.
(2)如图②,点P是线段AB上一点,射线EP交直线l₂于点F,∠GBE = 130°.
①若∠EFC = 40°,请求出∠FEA的度数;
②点N在射线AD上,且满足∠EBN = ∠EFC,连接BN,请补全图形,探究∠BNA与∠FEA满足的等量关系,并说明理由.
　　

答案：
[解]
(1)l₁//l₂
分析:因为AD平分∠BAC,所以∠BAC = 2∠BAE.
因为∠GBE = 2∠BAE,所以∠GBE =∠BAC,
所以l₁//l₂
(2)①因为∠GBE = 130°,
所以∠BAE = $\frac{1}{2}$∠GBE = 65°,∠ABE = 180° -∠GBE = 50°.因为l₁//l₂,所以∠BAF =∠ABE = 50°,
所以∠EAF =∠BAF +∠BAE = 115°,
所以∠FEA = 180° -∠EFC -∠EAF = 25°.
②∠BNA +∠FEA = 130°或∠BNA =∠FEA.
理由:当点N在线段AE上时，如图①所示,
由①知,∠FAE = 115°,所以∠EAC = 65°.
因为l₁//l₂所以∠BEF =∠EFC
因为∠EBN +∠BEN +∠BNE = 180°,∠BNE +∠BNA = 180°,所以∠EBN +∠BEF +∠FEA =∠BNA.
因为∠EBN =∠EFC,
所以2∠EFC +∠FEA =∠BNA.
易得∠EFC =∠EAC -∠FEA,即∠EFC = 65° -∠FEA,
所以130° - 2∠FEA +∠FEA =∠BNA,
所以∠BNA +∠FEA = 130°.
当点N在射线ED上时，如图②所示，
因为l₁//l₂,所以∠BEF =∠EFC.
因为∠EBN =∠EFC,所以∠BEF =∠EBN,
所以EF//BN.所以∠BNA =∠FEA.
综上,∠BNA +∠FEA = 130°或∠BNA =∠FEA.