《2025年真题圈七年级数学下册北师大版陕西专版》

15.(月考·23 - 24陕师大附中改编)(5分)计算:
(1)$300^{2}-297\times303$.
(2)$(2x + z - y)(2x - y + z)$.

答案：
(1)300²−297×303
=300²−(300−3)×(300+3)
=300²−(300²−9)
=300²−300²+9
=9.
(2)(2x+z−y)(2x−y+z)
=(2x−y+z)²
=(2x−y)²+2(2x−y)z+z²
=4x²−4xy+y²+4xz−2yz+z².

16.(期中·22 - 23西工大附中)(5分)先化简,再求值:$[(2x - y)^{2}-(y + 2x)(y - 2x)]\div(-\frac{1}{2}x)$,其中$x = (\pi - 3)^{0}$,$y = (-\frac{1}{3})^{-1}$.

答案： 原式=(4x²−4xy+y²−y²+4x²)÷(-$\frac{1}{2}$x)
=(8x²−4xy)÷(-$\frac{1}{2}$x)
=−16x+8y,
当x=(π−3)⁰=1,y=(-$\frac{1}{3}$)⁻¹=−3时,
原式=−16−24=−40.

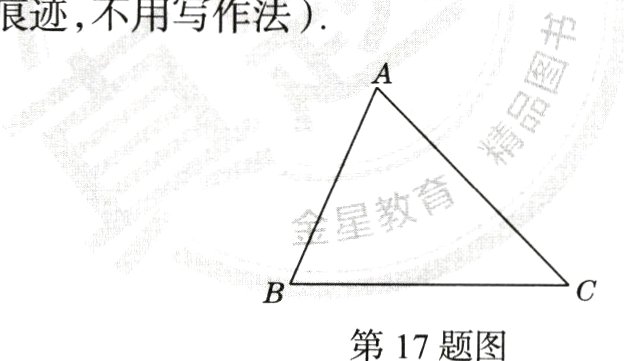
17.(月考·23 - 24西安滨河学校)(5分)如图,在$\triangle ABC$中,用尺规作图过点A作直线AD,使$AD// BC$(保留作图痕迹,不用写作法).

答案： 如图，直线AD即所求.

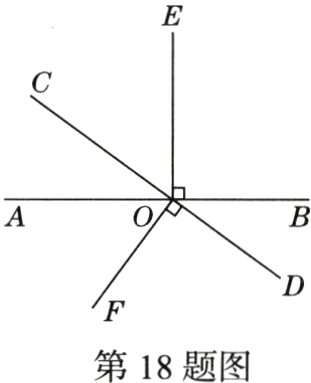
18.(月考·21 - 22西安铁一中)(5分)如图,直线AB与CD相交于点O,$OE\perp AB$,$OF\perp CD$.
(1)图中与∠AOF互余的角是____________________,与∠COE互补的角是______________________.(把符合条件的角都写出来)
(2)如果$\angle AOC=\frac{1}{4}\angle EOF$,求∠EOF的度数.

答案：
(1)∠AOC,∠BOD　∠EOD,∠BOF
(2)因为OE⊥AB,OF⊥CD,所以∠EOB=90°,∠FOD=90°.设∠AOC=x,则∠BOD=x
因为∠AOC=$\frac{1}{4}$∠EOF,所以∠EOF=4x.
根据题意可得4x+x+90°+90°=360°,解得x=36°.
所以∠EOF=4x=144°.