《2026年通城学典全国中考试题分类精粹中考数学》

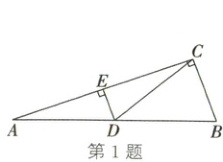
1. (2025·陕西)如图,在$\triangle ABC$中,$\angle ACB=90^{\circ}$,$\angle A=20^{\circ}$,$CD$为$AB$边上的中线,$DE\perp AC$于点$E$,则图中与$\angle A$互余的角共有(C)

A.2个
B.3个
C.4个
D.5个

答案： 1.C

2. (2025·威海)如图,直线$CF// DE$,$\angle ACB=90^{\circ}$,$\angle A=30^{\circ}$.若$\angle 1=18^{\circ}$,则$\angle 2$的度数为(A)

A.$42^{\circ}$
B.$38^{\circ}$
C.$36^{\circ}$
D.$30^{\circ}$

答案： 2.A

3. (2024·浙江)如图,正方形$ABCD$由四个全等的直角三角形($\mathrm{Rt}\triangle ABE$,$\mathrm{Rt}\triangle BCF$,$\mathrm{Rt}\triangle CDG$,$\mathrm{Rt}\triangle DAH$)和中间一个小正方形$EFGH$组成,连接$DE$.若$AE=4$,$BE=3$,则$DE$的长为(C)

A.5
B.$2\sqrt{6}$
C.$\sqrt{17}$
D.4

答案： 3.C

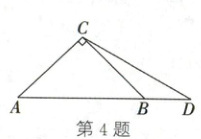
4. (2024·安徽)如图,在$\mathrm{Rt}\triangle ABC$中,$AC=BC=2$,点$D$在$AB$的延长线上,且$CD=AB$,则$BD$的长为(B)

A.$\sqrt{10}-\sqrt{2}$
B.$\sqrt{6}-\sqrt{2}$
C.$2\sqrt{2}-2$
D.$2\sqrt{2}-\sqrt{6}$

答案： 4.B

5. (2025·重庆)如图,正方形$ABCD$的边长为2,$E$是$BC$边的中点,连接$DE$,将$\triangle DCE$沿直线$DE$翻折到正方形$ABCD$所在的平面内,得$\triangle DFE$,延长$DF$交$AB$于点$G$.$\angle ADG$和$\angle DAG$的平分线$DH$,$AH$相交于点$H$,连接$GH$,则$\triangle DGH$的面积为(A)

A.$\dfrac{5}{8}$
B.$\dfrac{5}{4}$
C.$\dfrac{5\sqrt{5}}{8}$
D.$\dfrac{5\sqrt{5}}{4}$

答案：
5.A 解析：如图，连接GE.
∵四边形ABCD是正方形，$\therefore \angle B = \angle C = \angle BAD = \angle ADC = 90 ^ { \circ } , AB = BC = CD = DA = 2$.$\because E$是BC边的中点，$\therefore BE = CE = 1$.$\because$将$\triangle DCE$沿直线DE翻折得$\triangle DFE$，$\therefore \angle EFD = \angle C = 90 ^ { \circ }$，$CE = FE = BE = 1 , DC = DF = 2$.$\therefore \angle GFE = \angle GBE = 90 ^ { \circ }$．$\because GE = GE$，$\therefore Rt \triangle EFG \cong Rt \triangle EBG$．$\therefore GF = GB$.设$GB = GF = x$，则$AG = 2 - x$，$DG = 2 + x$.根据勾股定理，可得$AG ^ { 2 } + AD ^ { 2 } = DG ^ { 2 }$，即$(2 - x) ^ { 2 } + 2 ^ { 2 } = (2 + x) ^ { 2 }$，解得$x = \frac { 1 } { 2 }$.$\therefore DG = \frac { 5 } { 2 }$，$AG = \frac { 3 } { 2 }$.$\because \angle ADG$和$\angle DAG$的平分线DH，AH相交于点H，$\therefore$点H到AD，AG，GD的距离相等.设点H到AD的距离为h.$\therefore S _ { \triangle A G D } = S _ { \triangle A G H } + S _ { \triangle A D H } + S _ { \triangle G D H }$，即$\frac { 1 } { 2 } × \frac { 3 } { 2 } × 2 = \frac { 1 } { 2 } × \frac { 3 } { 2 } h + \frac { 1 } { 2 } × 2 h + \frac { 1 } { 2 } × \frac { 5 } { 2 } h$，解得$h = \frac { 1 } { 2 }$.$\therefore S _ { \triangle G D H } = \frac { 1 } { 2 } × \frac { 5 } { 2 } × \frac { 1 } { 2 } = \frac { 5 } { 8 }$.
　　　　　　　　

6. (2025·连云港)如图(单位:$\mathrm{m}$),长为$3\mathrm{m}$的梯子靠在墙上,梯子的底端离墙脚线的距离为$1.8\mathrm{m}$,则$h=$2.4.

答案： 6.2.4

7. (2025·福建)某房梁如图所示,立柱$AD\perp BC$,$E$,$F$分别是斜梁$AB$,$AC$的中点.若$AB=AC=8\mathrm{m}$,则$DE$的长为4$\mathrm{m}$.

答案： 7.4

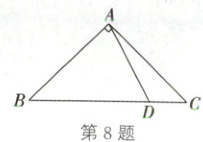
8. (2025·广安)如图,在等腰直角三角形$ABC$中,$\angle BAC=90^{\circ}$,$AB=AC=4$,$D$是$BC$边上的一个动点,连接$AD$,则$AD$长的最小值为$2 \sqrt { 2 }$.

答案： 8.$2 \sqrt { 2 }$

9. (2025·威海)把一张矩形纸片按照如图①所示的方式剪成四个全等的直角三角形,四个直角三角形可拼成如图②③所示的正方形.若矩形纸片的长为$m$,宽为$n$,四边形$EFGH$的面积等于四边形$ABCD$面积的2倍,则$\dfrac{m}{n}=$$\frac { 2 + \sqrt { 3 } } { 2 }$.

答案： 9.$\frac { 2 + \sqrt { 3 } } { 2 }$解析：由题意，得$m ^ { 2 } + ( \frac { n } { 2 } ) ^ { 2 } = 2 · ( m - \frac { 1 } { 2 } n ) ^ { 2 }$.整理，得$4 m ^ { 2 } - 8 m n + n ^ { 2 } = 0$，$\therefore m = \frac { 2 \pm \sqrt { 3 } } { 2 } n$．$\because m ＞ \frac { 1 } { 2 } n ＞ 0$，$\therefore \frac { m } { n } ＞ \frac { 1 } { 2 }$，$\therefore \frac { m } { n } = \frac { 2 + \sqrt { 3 } } { 2 }$