第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
10. (2025·山东)如图,在平面直角坐标系中,$A$,$C$两点在坐标轴上,四边形$OABC$是面积为$4$的正方形.若函数$y = \frac{k}{x}$($x > 0$)的图象经过点$B$,则满足$y \geq 2$的$x$的取值范围是(

A.$0 < x \leq 2$
B.$x \geq 2$
C.$0 < x \leq 4$
D.$x \geq 4$
A
)
A.$0 < x \leq 2$
B.$x \geq 2$
C.$0 < x \leq 4$
D.$x \geq 4$
答案:
10.A
11. (2025·湖北)已知蓄电池的电压为定值,使用蓄电池时,电流$I$(单位:$A$)与电阻$R$(单位:$\Omega$)是反比例函数关系,它的图象如图所示.当电阻大于$9 \Omega$时,电流可能是(
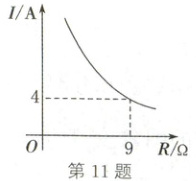
A.$3 A$
B.$4 A$
C.$5 A$
D.$6 A$
A
)
A.$3 A$
B.$4 A$
C.$5 A$
D.$6 A$
答案:
11.A
12. (2025·烟台)如图,菱形$OABC$的顶点$A$在$x$轴正半轴上,$OA = 3$,函数$y = \frac{k}{x}$($x > 0$)的图象过点$C$和菱形的对称中心$M$,则$k$的值为(
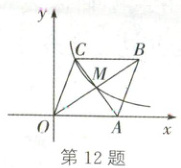
A.$4$
B.$4\sqrt{2}$
C.$2$
D.$2\sqrt{2}$
D
)
A.$4$
B.$4\sqrt{2}$
C.$2$
D.$2\sqrt{2}$
答案:
12.D解析:
∵菱形OABC的顶点A在x轴的正半轴上,OA=3,
∴AM=CM,OC=OA=3,A(3,0).设C(x,y),则M($\frac{x+3}{2}$,$\frac{y}{2}$).
∴xy=$\frac{x+3}{2}$·$\frac{y}{2}$,解得x=1.如图,过点C 作CH⊥AO于点H,则OH=1,CH= $\sqrt{OC²−OH²}$=$\sqrt{3²−1²}$=2$\sqrt{2}$
∴C(1,2$\sqrt{2}$).
∴k=1×2$\sqrt{2}$=2$\sqrt{2}$.

12.D解析:
∵菱形OABC的顶点A在x轴的正半轴上,OA=3,
∴AM=CM,OC=OA=3,A(3,0).设C(x,y),则M($\frac{x+3}{2}$,$\frac{y}{2}$).
∴xy=$\frac{x+3}{2}$·$\frac{y}{2}$,解得x=1.如图,过点C 作CH⊥AO于点H,则OH=1,CH= $\sqrt{OC²−OH²}$=$\sqrt{3²−1²}$=2$\sqrt{2}$
∴C(1,2$\sqrt{2}$).
∴k=1×2$\sqrt{2}$=2$\sqrt{2}$.

13. (2025·宜宾)如图,$O$是坐标原点,函数$y = -\frac{4}{x}$($x > 0$)的图象与直线$y = -2x$交于点$A$,点$B$在函数$y = -\frac{4}{x}$($x > 0$)的图象上,直线$AB$与$y$轴交于点$C$,连接$OB$.若$AB = 3AC$,则$OB$的长为(
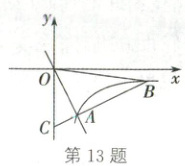
A.$\sqrt{10}$
B.$\frac{5\sqrt{2}}{2}$
C.$\sqrt{34}$
D.$\frac{\sqrt{130}}{2}$
D
)
A.$\sqrt{10}$
B.$\frac{5\sqrt{2}}{2}$
C.$\sqrt{34}$
D.$\frac{\sqrt{130}}{2}$
答案:
13.D解析:如图,过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E.
∵函数y=−$\frac{4}{x}$(x>0)的图象与直线y=−2x交于点A,
∴联立$\begin{cases} y=-\frac {4} {x}\\ y=-2x \end{cases}$解得$\begin{cases} x=\sqrt {2}\\ y=-2\sqrt {2} \end{cases}$或$\begin{cases} x=-\sqrt {2}\\ y=2\sqrt {2} \end{cases}$(舍去).
∴A($\sqrt{2}$,-2$\sqrt{2}$).
∴OD=$\sqrt{2}$.
∵AD⊥x轴,BE⊥x轴,
∴AD//BE.
∴$\frac{AB}{AC}$=$\frac{DE}{OD}$
∵AB=3AC,
∴3=$\frac{DE}{\sqrt{2}}$,即DE=3$\sqrt{2}$.
∴OE=OD+DE=$\sqrt{2}$+3$\sqrt{2}$=4$\sqrt{2}$.将x=4$\sqrt{2}$代入y=−$\frac{4}{x}$,得y=−$\frac{\sqrt{2}}{2}$.
∴BE=$\frac{\sqrt{2}}{2}$.
∴OB=$\sqrt{OE²+BE²}$=$\frac{\sqrt{130}}{2}$.

13.D解析:如图,过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E.
∵函数y=−$\frac{4}{x}$(x>0)的图象与直线y=−2x交于点A,
∴联立$\begin{cases} y=-\frac {4} {x}\\ y=-2x \end{cases}$解得$\begin{cases} x=\sqrt {2}\\ y=-2\sqrt {2} \end{cases}$或$\begin{cases} x=-\sqrt {2}\\ y=2\sqrt {2} \end{cases}$(舍去).
∴A($\sqrt{2}$,-2$\sqrt{2}$).
∴OD=$\sqrt{2}$.
∵AD⊥x轴,BE⊥x轴,
∴AD//BE.
∴$\frac{AB}{AC}$=$\frac{DE}{OD}$
∵AB=3AC,
∴3=$\frac{DE}{\sqrt{2}}$,即DE=3$\sqrt{2}$.
∴OE=OD+DE=$\sqrt{2}$+3$\sqrt{2}$=4$\sqrt{2}$.将x=4$\sqrt{2}$代入y=−$\frac{4}{x}$,得y=−$\frac{\sqrt{2}}{2}$.
∴BE=$\frac{\sqrt{2}}{2}$.
∴OB=$\sqrt{OE²+BE²}$=$\frac{\sqrt{130}}{2}$.

14. (2025·广西)如图,在平面直角坐标系中,“双曲线阶梯”$ABCDEFG$的所有线段均与$x$轴平行或垂直,且满足$BC = DE = FG = 1$,点$A$,$C$,$E$,$G$均在双曲线$y = \frac{k}{x}$的一支上.若点$A$的坐标为$(4,\frac{3}{2})$,则第三级阶梯的高$EF$等于(
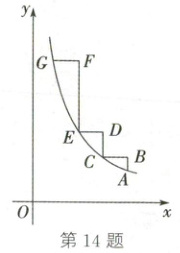
A.$4$
B.$3$
C.$\frac{7}{2}$
D.$\frac{5}{2}$
B
)
A.$4$
B.$3$
C.$\frac{7}{2}$
D.$\frac{5}{2}$
答案:
14.B解析:
∵点A(4,$\frac{3}{2}$)在双曲线y=$\frac{k}{x}$的一支上,
∴k=4×$\frac{3}{2}$=6.
∴反比例函数的解析式为y=$\frac{6}{x}$.
∵BC=1且BC与x轴平行,AB与y轴平行,点A的坐标为(4,$\frac{3}{2}$),
∴点C的横坐标比点A的横坐标小1,即横坐标为3.
∵点C在双曲线y=$\frac{6}{x}$的一支上,
∴当x=3时,y=2,即点C的坐标为(3,2).同理,可得点E的坐标为(2,3),点G的坐标为(1,6).观察题中图象可知,EF的长度等于点G的纵坐标减去点E的纵坐标,即EF=6−3=3.
∵点A(4,$\frac{3}{2}$)在双曲线y=$\frac{k}{x}$的一支上,
∴k=4×$\frac{3}{2}$=6.
∴反比例函数的解析式为y=$\frac{6}{x}$.
∵BC=1且BC与x轴平行,AB与y轴平行,点A的坐标为(4,$\frac{3}{2}$),
∴点C的横坐标比点A的横坐标小1,即横坐标为3.
∵点C在双曲线y=$\frac{6}{x}$的一支上,
∴当x=3时,y=2,即点C的坐标为(3,2).同理,可得点E的坐标为(2,3),点G的坐标为(1,6).观察题中图象可知,EF的长度等于点G的纵坐标减去点E的纵坐标,即EF=6−3=3.
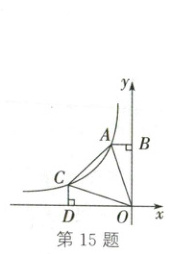
15. (2025·绥化)如图,函数$y = \frac{k}{x}$($x < 0$)的图象经过$A$,$C$两点,过点$A$作$AB \perp y$轴于点$B$,过点$C$作$CD \perp x$轴于点$D$,连接$OA$,$OC$,$AC$.若$S_{\triangle ACO} = 4$,$CD:OB = 1:3$,则$k$的值是(
A.$-12$
B.$-9$
C.$-6$
D.$-3$
D
)
A.$-12$
B.$-9$
C.$-6$
D.$-3$
答案:
15.D解析:如图,延长DC,BA交于点E.设CD=a(a>0).
∵CD:OB=1:3,
∴OB=3a.
∵AB⊥y轴,CD⊥x轴,
∴点A的纵坐标为3a,点C的纵坐标为a.
∴a=$\frac{k}{x_{C}}$,3a=$\frac{k}{x_{A}}$,
∴$x_{C}=\frac{k}{a}$,$x_{A}=\frac{k}{3a}$,
∴OD=$-\frac{k}{a}$,AB=$-\frac{k}{3a}$.
∵函数y=$\frac{k}{x}$(x<0)的图象经过A,C两点,
∴$S_{\triangle DOC}=S_{\triangle AOB}=-\frac{k}{2}$.
∵∠EDO=∠DOB=∠EBO=90°,
∴四边形OBED是矩形,BE=OD=$-\frac{k}{a}$,DE=OB=3a.
∴AE=BE−AB=$-\frac{k}{a}$−($-\frac{k}{3a}$)=$-\frac{2k}{3a}$,CE=DE−CD=3a−a=2a.
∴$S_{\triangle AEC}=\frac{1}{2}AE· CE=\frac{1}{2}·(-\frac{2k}{3a})·(2a)=-\frac{2k}{3}$.又
∵$S_{矩形OBED}=OD· OB=-\frac{k}{a}·3a=-3k$,$S_{\triangle AOD}=4$,$S_{矩形OBED}-S_{\triangle DOC}-S_{\triangle AOB}-S_{\triangle AEC}=S_{\triangle AOD}$,
∴$-3k-(-\frac{k}{2})-(-\frac{k}{2})-(-\frac{2k}{3})=4$,解得k=−3.

15.D解析:如图,延长DC,BA交于点E.设CD=a(a>0).
∵CD:OB=1:3,
∴OB=3a.
∵AB⊥y轴,CD⊥x轴,
∴点A的纵坐标为3a,点C的纵坐标为a.
∴a=$\frac{k}{x_{C}}$,3a=$\frac{k}{x_{A}}$,
∴$x_{C}=\frac{k}{a}$,$x_{A}=\frac{k}{3a}$,
∴OD=$-\frac{k}{a}$,AB=$-\frac{k}{3a}$.
∵函数y=$\frac{k}{x}$(x<0)的图象经过A,C两点,
∴$S_{\triangle DOC}=S_{\triangle AOB}=-\frac{k}{2}$.
∵∠EDO=∠DOB=∠EBO=90°,
∴四边形OBED是矩形,BE=OD=$-\frac{k}{a}$,DE=OB=3a.
∴AE=BE−AB=$-\frac{k}{a}$−($-\frac{k}{3a}$)=$-\frac{2k}{3a}$,CE=DE−CD=3a−a=2a.
∴$S_{\triangle AEC}=\frac{1}{2}AE· CE=\frac{1}{2}·(-\frac{2k}{3a})·(2a)=-\frac{2k}{3}$.又
∵$S_{矩形OBED}=OD· OB=-\frac{k}{a}·3a=-3k$,$S_{\triangle AOD}=4$,$S_{矩形OBED}-S_{\triangle DOC}-S_{\triangle AOB}-S_{\triangle AEC}=S_{\triangle AOD}$,
∴$-3k-(-\frac{k}{2})-(-\frac{k}{2})-(-\frac{2k}{3})=4$,解得k=−3.

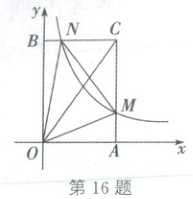
16. (2025·北京)如图,在平面直角坐标系中,$A$,$B$分别是横、纵轴正半轴上的动点,四边形$OACB$是矩形,函数$y = \frac{1}{x}$($x > 0$)的图象与边$AC$交于点$M$,与边$BC$交于点$N$($M$,$N$两点不重合).给出下列四个结论:
① $\triangle COM$与$\triangle CON$的面积一定相等;
② $\triangle MON$与$\triangle MCN$的面积可能相等;
③ $\triangle MON$一定是锐角三角形;
④ $\triangle MON$可能是等边三角形.
其中,正确的是(
A.①③
B.①④
C.②③
D.②④
① $\triangle COM$与$\triangle CON$的面积一定相等;
② $\triangle MON$与$\triangle MCN$的面积可能相等;
③ $\triangle MON$一定是锐角三角形;
④ $\triangle MON$可能是等边三角形.
其中,正确的是(
B
)
A.①③
B.①④
C.②③
D.②④
答案:
16.B解析:根据题意,设点M的坐标为(a,$\frac{1}{a}$),点N的坐标为(b,$\frac{1}{b}$),则A(a,0),B(0,$\frac{1}{b}$),C(a,$\frac{1}{b}$).
∴OB=AC=$\frac{1}{b}$,OA=BC=a,BN=b,AM=$\frac{1}{a}$,CN=a−b,CM=$\frac{1}{b}$-$\frac{1}{a}$.
∴$S_{\triangle COM}=\frac{1}{2}CM· OA=\frac{1}{2}(\frac{1}{b}-\frac{1}{a})· a=\frac{a}{2b}-\frac{1}{2}$,$S_{\triangle CON}=\frac{1}{2}CN· OB=\frac{1}{2}(a - b)·\frac{1}{b}=\frac{a}{2b}-\frac{1}{2}$,
∴$S_{\triangle COM}=S_{\triangle CON}$.故结论①正确.$S_{\triangle MCN}=\frac{1}{2}CN· CM=\frac{1}{2}(a - b)(\frac{1}{b}-\frac{1}{a})=\frac{(a - b)^{2}}{2ab}$,$S_{\triangle MON}=S_{矩形OACB}-S_{\triangle OBN}-S_{\triangle OAM}-S_{\triangle MCN}=a·\frac{1}{b}-\frac{1}{2}-\frac{1}{2}-\frac{(a - b)^{2}}{2ab}=\frac{a^{2}-b^{2}}{2ab}$.当$\triangle MON$与$\triangle MCN$的面积相等时,$\frac{(a - b)^{2}}{2ab}=\frac{a^{2}-b^{2}}{2ab}$,即a=b,此时M,N两点重合,与题意不符.故结论②错误.函数y=$\frac{1}{x}$(x>0)的图象是固定的,但矩形OACB不固定,可通过移动点A,B,得到直角三角形MON(如图①)或钝角三角形MON(如图②).故结论③错误.假设$\triangle MON$是等边三角形,则OM=ON=MN,且∠MON=60°,则$OM^{2}=ON^{2}$,即$a^{2}+(\frac{1}{a})^{2}=b^{2}+(\frac{1}{b})^{2}$.整理,得$a^{2}-b^{2}+\frac{1}{a^{2}}-\frac{1}{b^{2}}=0$,即$(a^{2}-b^{2})(1-\frac{1}{a^{2}b^{2}})=0$.
∵a≠b (M,N两点不重合),
∴$1-\frac{1}{a^{2}b^{2}}=0$,
∴$a^{2}b^{2}=1$,
∴ab = 1,
∴$a=\frac{1}{b}$,
∴B(0,a).又
∵A(a,0),
∴OA=OB.
∴当矩形OACB是正方形,∠AOM=∠BON=15°时,$\triangle MON$是等边三角形(如图③).故结论④正确.综上所述,①④正确



16.B解析:根据题意,设点M的坐标为(a,$\frac{1}{a}$),点N的坐标为(b,$\frac{1}{b}$),则A(a,0),B(0,$\frac{1}{b}$),C(a,$\frac{1}{b}$).
∴OB=AC=$\frac{1}{b}$,OA=BC=a,BN=b,AM=$\frac{1}{a}$,CN=a−b,CM=$\frac{1}{b}$-$\frac{1}{a}$.
∴$S_{\triangle COM}=\frac{1}{2}CM· OA=\frac{1}{2}(\frac{1}{b}-\frac{1}{a})· a=\frac{a}{2b}-\frac{1}{2}$,$S_{\triangle CON}=\frac{1}{2}CN· OB=\frac{1}{2}(a - b)·\frac{1}{b}=\frac{a}{2b}-\frac{1}{2}$,
∴$S_{\triangle COM}=S_{\triangle CON}$.故结论①正确.$S_{\triangle MCN}=\frac{1}{2}CN· CM=\frac{1}{2}(a - b)(\frac{1}{b}-\frac{1}{a})=\frac{(a - b)^{2}}{2ab}$,$S_{\triangle MON}=S_{矩形OACB}-S_{\triangle OBN}-S_{\triangle OAM}-S_{\triangle MCN}=a·\frac{1}{b}-\frac{1}{2}-\frac{1}{2}-\frac{(a - b)^{2}}{2ab}=\frac{a^{2}-b^{2}}{2ab}$.当$\triangle MON$与$\triangle MCN$的面积相等时,$\frac{(a - b)^{2}}{2ab}=\frac{a^{2}-b^{2}}{2ab}$,即a=b,此时M,N两点重合,与题意不符.故结论②错误.函数y=$\frac{1}{x}$(x>0)的图象是固定的,但矩形OACB不固定,可通过移动点A,B,得到直角三角形MON(如图①)或钝角三角形MON(如图②).故结论③错误.假设$\triangle MON$是等边三角形,则OM=ON=MN,且∠MON=60°,则$OM^{2}=ON^{2}$,即$a^{2}+(\frac{1}{a})^{2}=b^{2}+(\frac{1}{b})^{2}$.整理,得$a^{2}-b^{2}+\frac{1}{a^{2}}-\frac{1}{b^{2}}=0$,即$(a^{2}-b^{2})(1-\frac{1}{a^{2}b^{2}})=0$.
∵a≠b (M,N两点不重合),
∴$1-\frac{1}{a^{2}b^{2}}=0$,
∴$a^{2}b^{2}=1$,
∴ab = 1,
∴$a=\frac{1}{b}$,
∴B(0,a).又
∵A(a,0),
∴OA=OB.
∴当矩形OACB是正方形,∠AOM=∠BON=15°时,$\triangle MON$是等边三角形(如图③).故结论④正确.综上所述,①④正确



查看更多完整答案,请扫码查看


