第169页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
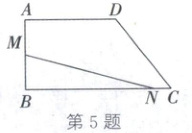
5. (2025·天津)在四边形$ABCD$中,$AD// BC$,$\angle B = 90^{\circ}$,$AB = 8\ cm$,$AD = 10\ cm$,$BC = 16\ cm$.动点$M$从点$B$出发,以$2\ cm/s$的速度沿边$BA$,$AD$向终点$D$运动;动点$N$从点$C$同时出发,以$1\ cm/s$的速度沿边$CB$向终点$B$运动.规定其中一个动点到达终点时,另一个动点也随之停止运动.设运动的时间为$t\ s$.当$t = 2$时,点$M$,$N$的位置如图所示.有下列结论:①当$t = 6$时,$CN = DM$;②当$1\leq t\leq 2$时,$\triangle BMN$的最大面积为$26\ cm^{2}$;③$t$有两个不同的值满足$\triangle BMN$的面积为$39\ cm^{2}$.其中,正确的个数是(
A.$0$
B.$1$
C.$2$
D.$3$
C
)
A.$0$
B.$1$
C.$2$
D.$3$
答案:
C 解析:根据题意,得点$M$在$AB$上的运动时间为$8÷2=4(s)$,点$M$在$AD$上的运动时间为$10÷2=5(s).\because16÷1=16(s),4 + 5 = 9(s),16>9,\therefore$点$N$在$CB$上的运动时间为$9s$.①当$t = 6$时,点$M$在$AD$上,此时$AM = 2×6 - 8 = 4(cm),CN = 6cm,\therefore DM = AD - AM = 6cm.\therefore CN = DM$.故①正确.②当$1\leq t\leq2$时,点$M$在$AB$上,此时$BM = 2tcm,CN = tcm,\therefore BN = (16 - t)cm$.设$S_{\triangle BMN}=ycm^2$.$\because S_{\triangle BMN}=\frac{1}{2}BM· BN,\therefore y=\frac{1}{2}×2t(16 - t)=-t^{2}+16t=-(t - 8)^{2}+64.\because - 1<0,\therefore$当$t<8$时,$y$随$t$的增大而增大.$\therefore$当$t = 2$时,$y$取得最大值,为$-(2 - 8)^{2}+64 = 28.\therefore$当$1\leq t\leq2$时,$\triangle BMN$的最大面积为$28cm^2$.故②错误.③当点$M$在$AB$上时,若$\triangle BMN$的面积为$39cm^2$,则令$y=-t^{2}+16t = 39$,解得$t_{1}=3,t_{2}=13$(舍去).$\therefore$当$t = 3$时,$\triangle BMN$的面积为$39cm^2$.当点$M$在$AD$上时,$\because AD// BC,\angle B = 90^{\circ},\therefore\angle A = 180^{\circ}-\angle B = 90^{\circ}$,即$AB\bot AD$.此时$S_{\triangle BMN}=\frac{1}{2}AB· BN,\therefore y=\frac{1}{2}×8(16 - t)=64 - 4t$.若$\triangle BMN$的面积为$39cm^2$,则令$y = 64 - 4t = 39$,解得$t=\frac{25}{4}$.$\therefore$当$t=\frac{25}{4}$时,$\triangle BMN$的面积为$39cm^2.\therefore t$有两个不同的值满足$\triangle BMN$的面积为$39cm^2$.故③正确.综上所述,正确的个数是$2$.
6. (2025·内江)如图,在矩形$ABCD$中,$AB = 8$,$AD = 6$,$E$,$F$分别是边$AD$,$CD$上的动点,连接$BE$,$EF$,$G$为$BE$的中点,$H$为$EF$的中点,连接$GH$,则$GH$长的最大值是

5
.
答案:
5
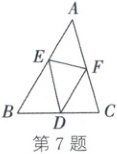
7. (2025·内江)如图,在$\triangle ABC$中,$\angle A = 45^{\circ}$,$\angle B = 60^{\circ}$,$AB = 2\sqrt{2}$,$D$,$E$,$F$分别是边$BC$,$AB$,$AC$上的动点,则$\triangle DEF$的周长最小为
$2\sqrt{3}$
.
答案:
7.$2\sqrt{3}$ 解析:如图,作点$D$关于$AB,AC$的对称点$N,M$,连接$AM,AN,EN,FM,MN,AD$,则$EN = ED,FM = FD$,$\angle NAE=\angle DAE,\angle MAF=\angle DAF,AN = AD = AM$.$\therefore\triangle DEF$的周长为$DE + EF + FD = NE + EF + FM\geqslant MN.\therefore$当$N,E,F,M$四点共线时,$\triangle DEF$的周长取得最小值,为线段$MN$的长.$\because\angle NAM=\angle NAE+\angle DAE+\angle MAF+\angle DAF=2(\angle DAE+\angle DAF)=2\angle EAF = 90^{\circ}$,且$AN = AM,\therefore\triangle AMN$是等腰直角三角形.$\therefore$易得$MN=\sqrt{2}AN=\sqrt{2}AD.\therefore$当$AD\bot BC$时,$AD$的长取得最小值,即$MN$的长取得最小值,此时$\triangle DEF$的周长最小.又$\because\angle B = 60^{\circ},AB = 2\sqrt{2},\therefore$当$AD\bot BC$时,$AD = AB·\sin60^{\circ}=2\sqrt{2}×\frac{\sqrt{3}}{2}=\sqrt{6}$,此时$MN=\sqrt{2}AD = 2\sqrt{3}$.$\therefore\triangle DEF$的周长最小为$2\sqrt{3}$.

7.$2\sqrt{3}$ 解析:如图,作点$D$关于$AB,AC$的对称点$N,M$,连接$AM,AN,EN,FM,MN,AD$,则$EN = ED,FM = FD$,$\angle NAE=\angle DAE,\angle MAF=\angle DAF,AN = AD = AM$.$\therefore\triangle DEF$的周长为$DE + EF + FD = NE + EF + FM\geqslant MN.\therefore$当$N,E,F,M$四点共线时,$\triangle DEF$的周长取得最小值,为线段$MN$的长.$\because\angle NAM=\angle NAE+\angle DAE+\angle MAF+\angle DAF=2(\angle DAE+\angle DAF)=2\angle EAF = 90^{\circ}$,且$AN = AM,\therefore\triangle AMN$是等腰直角三角形.$\therefore$易得$MN=\sqrt{2}AN=\sqrt{2}AD.\therefore$当$AD\bot BC$时,$AD$的长取得最小值,即$MN$的长取得最小值,此时$\triangle DEF$的周长最小.又$\because\angle B = 60^{\circ},AB = 2\sqrt{2},\therefore$当$AD\bot BC$时,$AD = AB·\sin60^{\circ}=2\sqrt{2}×\frac{\sqrt{3}}{2}=\sqrt{6}$,此时$MN=\sqrt{2}AD = 2\sqrt{3}$.$\therefore\triangle DEF$的周长最小为$2\sqrt{3}$.

8. (2025·烟台)如图,在菱形$ABCD$中,$\angle BAD = 60^{\circ}$,对角线$AC = 6\ cm$.点$M$从点$A$出发,沿$AC$方向以$1\ cm/s$的速度向点$C$运动,同时,点$N$从点$C$出发,沿$CD$方向以$\sqrt{3}\ cm/s$的速度向点$D$运动,当一点到达终点时,另一点随之停止运动,连接$AN$,$DM$交于点$P$.在此过程中,点$P$的运动路径长为

$\frac{2\sqrt{3}\pi}{3}$
$cm$.
答案:
8.$\frac{2\sqrt{3}\pi}{3}$ 解析:如图,连接$BD$交$AC$于点$J.\because$在菱形$ABCD$中,$\angle BAD = 60^{\circ},AC = 6cm,\therefore AC\bot BD,\angle DAC = 30^{\circ}=\angle DCA,AJ = CJ = 3cm.\therefore DJ = BJ = AJ·\tan30^{\circ}=\sqrt{3}cm.\therefore AD = 2DJ = 2\sqrt{3}cm$.设运动时间为$ts$,则$AM = tcm,CN=\sqrt{3}tcm.\because\frac{t}{2\sqrt{3}}=\frac{\sqrt{3}t}{6}$,即$\frac{AM}{AD}=\frac{CN}{CA}$,且$\angle DAM=\angle ACN,\therefore\triangle ADM\sim\triangle CAN.\therefore\angle ADM=\angle CAN.\therefore\angle APM=\angle DAP+\angle ADM=\angle DAP+\angle CAN=\angle DAC = 30^{\circ}.\therefore\angle APD = 180^{\circ}-30^{\circ}=150^{\circ}$.以$AD$为边,在菱形$ABCD$外作等边三角形$ADO$,以点$O$为圆心,$OD$为半径作圆,在$\odot O$上取一点$K$,连接$AK,DK$.$\therefore OA = OD = AD = 2\sqrt{3}cm,\angle AOD = 60^{\circ},\angle AKD=\frac{1}{2}×60^{\circ}=30^{\circ}.\therefore\angle AKD+\angle APD = 180^{\circ}.$点$P$在$\odot O$上的$\stackrel\frown{AD}$上.$\therefore$在此过程中,点$P$的运动路径长为$\frac{60\pi×2\sqrt{3}}{180}=\frac{2\sqrt{3}\pi}{3}(cm)$.

8.$\frac{2\sqrt{3}\pi}{3}$ 解析:如图,连接$BD$交$AC$于点$J.\because$在菱形$ABCD$中,$\angle BAD = 60^{\circ},AC = 6cm,\therefore AC\bot BD,\angle DAC = 30^{\circ}=\angle DCA,AJ = CJ = 3cm.\therefore DJ = BJ = AJ·\tan30^{\circ}=\sqrt{3}cm.\therefore AD = 2DJ = 2\sqrt{3}cm$.设运动时间为$ts$,则$AM = tcm,CN=\sqrt{3}tcm.\because\frac{t}{2\sqrt{3}}=\frac{\sqrt{3}t}{6}$,即$\frac{AM}{AD}=\frac{CN}{CA}$,且$\angle DAM=\angle ACN,\therefore\triangle ADM\sim\triangle CAN.\therefore\angle ADM=\angle CAN.\therefore\angle APM=\angle DAP+\angle ADM=\angle DAP+\angle CAN=\angle DAC = 30^{\circ}.\therefore\angle APD = 180^{\circ}-30^{\circ}=150^{\circ}$.以$AD$为边,在菱形$ABCD$外作等边三角形$ADO$,以点$O$为圆心,$OD$为半径作圆,在$\odot O$上取一点$K$,连接$AK,DK$.$\therefore OA = OD = AD = 2\sqrt{3}cm,\angle AOD = 60^{\circ},\angle AKD=\frac{1}{2}×60^{\circ}=30^{\circ}.\therefore\angle AKD+\angle APD = 180^{\circ}.$点$P$在$\odot O$上的$\stackrel\frown{AD}$上.$\therefore$在此过程中,点$P$的运动路径长为$\frac{60\pi×2\sqrt{3}}{180}=\frac{2\sqrt{3}\pi}{3}(cm)$.

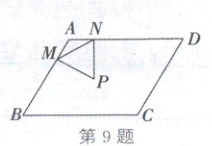
9. (2025·陕西)如图,在$□ ABCD$中,$AB = 6$,$AD = 8$,$\angle B = 60^{\circ}$.动点$M$,$N$分别在边$AB$,$AD$上,且$AM = AN$,以$MN$为边作等边三角形$MNP$,使点$P$始终在$□ ABCD$的内部或边上.当$\triangle MNP$的面积最大时,$DN$的长为
5
.
答案:
9.5 解析:连接$AP$并延长,交$BC$于点$H.\because$四边形$ABCD$是平行四边形,$\angle B = 60^{\circ},\therefore$易知$\angle BAD = 120^{\circ}$.$\because\triangle MNP$是等边三角形,$\therefore MP = PN,\angle MPN = 60^{\circ}$,易知$S_{\triangle MNP}=\frac{\sqrt{3}}{4}MP^{2}.\because AM = AN,AP = AP,\therefore\triangle AMP\cong\triangle ANP.\therefore\angle BAP=\angle DAP = 60^{\circ},\angle APM=\angle APN = 30^{\circ}.\therefore\angle AMP = 90^{\circ}.\therefore MP=\sin60^{\circ}· AP=\frac{\sqrt{3}}{2}AP$.$\therefore S_{\triangle MNP}=\frac{\sqrt{3}}{4}×(\frac{\sqrt{3}}{2}AP)^{2}=\frac{3\sqrt{3}}{16}AP^{2}.\therefore$当$AP$的长最大时,$\triangle MNP$的面积最大.$\because\angle B=\angle BAH = 60^{\circ},\therefore$易知$\triangle ABH$是等边三角形.$\therefore AB = AH = 6.\because\angle BAP = 60^{\circ}$,$\therefore$点$P$在$AH$上运动.$\because$点$P$始终在$□ ABCD$的内部或边上,$\therefore AP$长的最大值为$AH$的长,即$AP = 6$.此时易得$AM = AN=\frac{1}{2}AP = 3.\therefore DN = AD - AN = 5$.
10. (2025·连云港)如图,在菱形$ABCD$中,$AC = 4$,$BD = 2$,$E$为线段$AC$上的动点,四边形$DAEF$为平行四边形,则$BE + BF$的最小值为

$\sqrt{13}$
.
答案:
10.$\sqrt{13}$ 解析:$\because$四边形$DAEF$为平行四边形,$\therefore EF = AD,DF = AE.\because E$为线段$AC$上的动点,$\therefore$可以将$EF$看作是定线段,菱形$ABCD$在$AC$方向上水平运动.如图①,点$B$的运动轨迹为线段$MN$,作点$E$关于线段$MN$的对称点$E^{\prime}$,连接$BE^{\prime},E^{\prime}F$.由对称,得$BE = BE^{\prime},\therefore BE + BF = BE^{\prime}+BF\leqslant E^{\prime}F$,当且仅当$E^{\prime},B,F$三点依次共线时,$B^{\prime}E + BF$取得最小值,为$E^{\prime}F$的长.此时如图②,设$AC$与$BD$交于点$O,EE^{\prime}$交$MN$于点$H$,延长$E^{\prime}E$交$FD$的延长线于点$G$.在菱形$ABCD$中,$AC = 4,BD = 2,\therefore AO=\frac{1}{2}AC = 2,BO = DO=\frac{1}{2}BD = 1,AC\bot BD$.由题意,得$AC// MN$.由对称,可得$EH = E^{\prime}H,EH\bot HB.\therefore\angle GEO=\angle OEH=\angle EOB=\angle EHB = 90^{\circ}.\therefore$四边形$EOBH$是矩形.$\therefore EH = E^{\prime}H = OB = 1.\because$四边形$DAEF$为平行四边形,$\therefore DF// AC.\therefore GD\bot DO.\therefore\angle GDO=\angle DOE=\angle GEO = 90^{\circ}.$四边形$DOEG$是矩形.$\therefore GD = EO,GE = DO = 1.\therefore GF = GD + DF = EO + AE = AO = 2,GE^{\prime}=GE + EH + E^{\prime}H = 3.\therefore E^{\prime}F=\sqrt{GF^{2}+GE^{\prime2}}=\sqrt{2^{2}+3^{2}}=\sqrt{13}$,即$BE + BF$的最小值为$\sqrt{13}$.

10.$\sqrt{13}$ 解析:$\because$四边形$DAEF$为平行四边形,$\therefore EF = AD,DF = AE.\because E$为线段$AC$上的动点,$\therefore$可以将$EF$看作是定线段,菱形$ABCD$在$AC$方向上水平运动.如图①,点$B$的运动轨迹为线段$MN$,作点$E$关于线段$MN$的对称点$E^{\prime}$,连接$BE^{\prime},E^{\prime}F$.由对称,得$BE = BE^{\prime},\therefore BE + BF = BE^{\prime}+BF\leqslant E^{\prime}F$,当且仅当$E^{\prime},B,F$三点依次共线时,$B^{\prime}E + BF$取得最小值,为$E^{\prime}F$的长.此时如图②,设$AC$与$BD$交于点$O,EE^{\prime}$交$MN$于点$H$,延长$E^{\prime}E$交$FD$的延长线于点$G$.在菱形$ABCD$中,$AC = 4,BD = 2,\therefore AO=\frac{1}{2}AC = 2,BO = DO=\frac{1}{2}BD = 1,AC\bot BD$.由题意,得$AC// MN$.由对称,可得$EH = E^{\prime}H,EH\bot HB.\therefore\angle GEO=\angle OEH=\angle EOB=\angle EHB = 90^{\circ}.\therefore$四边形$EOBH$是矩形.$\therefore EH = E^{\prime}H = OB = 1.\because$四边形$DAEF$为平行四边形,$\therefore DF// AC.\therefore GD\bot DO.\therefore\angle GDO=\angle DOE=\angle GEO = 90^{\circ}.$四边形$DOEG$是矩形.$\therefore GD = EO,GE = DO = 1.\therefore GF = GD + DF = EO + AE = AO = 2,GE^{\prime}=GE + EH + E^{\prime}H = 3.\therefore E^{\prime}F=\sqrt{GF^{2}+GE^{\prime2}}=\sqrt{2^{2}+3^{2}}=\sqrt{13}$,即$BE + BF$的最小值为$\sqrt{13}$.

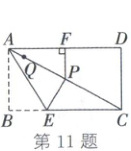
11. (2025·扬州)如图,在矩形$ABCD$中,$AB = 4$,$BC = 4\sqrt{3}$,$E$是边$BC$上的动点,将$\triangle ABE$沿直线$AE$翻折得到$\triangle APE$,过点$P$作$PF\perp AD$,垂足为$F$,$Q$是线段$AP$上一点,且$AQ = \frac{1}{2}PF$.当点$E$从点$B$运动到点$C$时,点$Q$运动的路径长是
$\frac{4\pi}{3}$
.
答案:
11.$\frac{4\pi}{3}$ 解析:$\because$四边形$ABCD$是矩形,$\therefore\angle BAD=\angle B = 90^{\circ}.\because$将$\triangle ABE$沿直线$AE$翻折得到$\triangle APE$,$\therefore AP = AB = 4$.当点$P$在矩形内部时,如图①,作$HQ\bot AP$,交$AB$于点$H$,则$\angle AQH = 90^{\circ}=\angle BAD.\therefore\angle AHQ=\angle PAF = 90^{\circ}-\angle HAQ.\because PF\bot AD,\therefore\angle PFA = 90^{\circ}=\angle AQH.\therefore\triangle AQH\sim\triangle PFA.\therefore\frac{AH}{PA}=\frac{AQ}{PF}.\because AQ=\frac{1}{2}PF,\therefore\frac{AH}{AP}=\frac{AQ}{PF}=\frac{1}{2}.\therefore AH=\frac{1}{2}AP = 2.\therefore$点$Q$在以$AH$为直径的圆上运动.$\therefore$当点$E$从点$B$开始运动直至点$P$落在$AD$上时,点$Q$的运动轨迹为半圆$AH.\therefore$这段内点$Q$的运动路径长为$\frac{1}{2}×2\pi=\pi$.当点$P$在矩形外部时,如图②,作$KQ\bot AP$,交$BA$的延长线于点$K$.同理可得$\triangle AKQ\sim\triangle PAF,AK=\frac{1}{2}AP = 2.\therefore\angle AKQ=\angle PAF$,点$Q$在以$AK$为直径的圆上运动.记圆心为$O$,连接$OQ$.当点$E$运动到点$C$时,$\because AB = 4,BC = 4\sqrt{3},\angle B = 90^{\circ}$,$\therefore\tan\angle BAC=\frac{BC}{AB}=\sqrt{3}.\therefore\angle BAC = 60^{\circ}.\therefore\angle CAD=\angle BAD-\angle BAC = 30^{\circ}.\because$将$\triangle ABE$沿直线$AE$翻折得到$\triangle APE,\therefore\angle PAC=\angle BAC = 60^{\circ}.\therefore\angle PAF=\angle PAC-\angle CAD = 30^{\circ}.\therefore\angle AKQ=\angle PAF = 30^{\circ}.\therefore\angle AOQ=2\angle AKQ = 60^{\circ}.\therefore$点$Q$的运动轨迹为所对圆心角为$60^{\circ}$的$\stackrel\frown{AQ}$.这段内点$Q$的运动路径长为$\frac{60\pi}{180}×1=\frac{\pi}{3}.\therefore$点$Q$的运动路径总长为$\pi+\frac{\pi}{3}=\frac{4\pi}{3}$.

11.$\frac{4\pi}{3}$ 解析:$\because$四边形$ABCD$是矩形,$\therefore\angle BAD=\angle B = 90^{\circ}.\because$将$\triangle ABE$沿直线$AE$翻折得到$\triangle APE$,$\therefore AP = AB = 4$.当点$P$在矩形内部时,如图①,作$HQ\bot AP$,交$AB$于点$H$,则$\angle AQH = 90^{\circ}=\angle BAD.\therefore\angle AHQ=\angle PAF = 90^{\circ}-\angle HAQ.\because PF\bot AD,\therefore\angle PFA = 90^{\circ}=\angle AQH.\therefore\triangle AQH\sim\triangle PFA.\therefore\frac{AH}{PA}=\frac{AQ}{PF}.\because AQ=\frac{1}{2}PF,\therefore\frac{AH}{AP}=\frac{AQ}{PF}=\frac{1}{2}.\therefore AH=\frac{1}{2}AP = 2.\therefore$点$Q$在以$AH$为直径的圆上运动.$\therefore$当点$E$从点$B$开始运动直至点$P$落在$AD$上时,点$Q$的运动轨迹为半圆$AH.\therefore$这段内点$Q$的运动路径长为$\frac{1}{2}×2\pi=\pi$.当点$P$在矩形外部时,如图②,作$KQ\bot AP$,交$BA$的延长线于点$K$.同理可得$\triangle AKQ\sim\triangle PAF,AK=\frac{1}{2}AP = 2.\therefore\angle AKQ=\angle PAF$,点$Q$在以$AK$为直径的圆上运动.记圆心为$O$,连接$OQ$.当点$E$运动到点$C$时,$\because AB = 4,BC = 4\sqrt{3},\angle B = 90^{\circ}$,$\therefore\tan\angle BAC=\frac{BC}{AB}=\sqrt{3}.\therefore\angle BAC = 60^{\circ}.\therefore\angle CAD=\angle BAD-\angle BAC = 30^{\circ}.\because$将$\triangle ABE$沿直线$AE$翻折得到$\triangle APE,\therefore\angle PAC=\angle BAC = 60^{\circ}.\therefore\angle PAF=\angle PAC-\angle CAD = 30^{\circ}.\therefore\angle AKQ=\angle PAF = 30^{\circ}.\therefore\angle AOQ=2\angle AKQ = 60^{\circ}.\therefore$点$Q$的运动轨迹为所对圆心角为$60^{\circ}$的$\stackrel\frown{AQ}$.这段内点$Q$的运动路径长为$\frac{60\pi}{180}×1=\frac{\pi}{3}.\therefore$点$Q$的运动路径总长为$\pi+\frac{\pi}{3}=\frac{4\pi}{3}$.

12. (2025·绥化)在边长为$7$的等边三角形$ABC$中,点$D$在$AB$上,$BD = 2$.$M$是直线$BC$上的一个动点,连接$MD$,以$MD$为一边在$MD$的左侧作等边三角形$MND$,连接$BN$.当$\triangle BND$为直角三角形时,$CM$的长是
6或8或9
.
答案:
12.6或8或9 解析:过点$D$作$DE// AC$,交$BC$于点$E$.当$\angle DBN = 90^{\circ}$且点$M$在$CB$的延长线上时,如图①$\because\triangle ABC$是等边三角形,$DE// AC,\therefore$易得$\triangle BDE$是等边三角形.$\therefore DE = DB = 2,\angle BDE = 60^{\circ}.\because\triangle DMN$是等边三角形,$\therefore DN = DM,\angle NDM = 60^{\circ}.\therefore\angle BDE=\angle NDM.\therefore$易得$\angle EDN=\angle BDM.\therefore\triangle DEN\cong\triangle DBM.\therefore\angle DEN=\angle DBM = 180^{\circ}-60^{\circ}=120^{\circ},EN = BM.\because$易得$\angle DEB=\angle DBE = 60^{\circ},\therefore\angle BEN=\angle DEN-\angle DEB = 60^{\circ},\angle NBE=\angle DBN-\angle DBE = 30^{\circ}.\therefore\angle BNE = 90^{\circ}.\therefore EN=\frac{1}{2}BE = 1.\therefore BM = 1.\therefore MC = BC + BM = 7 + 1 = 8$.当$\angle BDN = 90^{\circ}$且点$M$在$BC$上时,如图②.同理可得$\triangle DEN\cong\triangle DBM,\angle NDE=\angle BDN-\angle BDE = 90^{\circ}-60^{\circ}=30^{\circ},\therefore\angle NED=\angle MBD = 60^{\circ},\angle DMB=\angle DNE = 90^{\circ}.\therefore BM = BD·\cos60^{\circ}=2×\frac{1}{2}=1.\therefore CM = BC - BM = 6$.当$\angle BND = 90^{\circ}$且点$M$在$CB$上时,如图③.同理可证$\triangle DBN\cong\triangle DEM,DE = BD = 2,\angle DEM = 60^{\circ}$,$\therefore\angle DME=\angle DNB = 90^{\circ}.\therefore ME = DE·\cos60^{\circ}=2×\frac{1}{2}=1.\therefore BM = 1.\therefore CM = BC - BM = 6$.当$\angle BND = 90^{\circ}$且点$M$在$CB$的延长线上时,如图④.同理可证$\triangle DBN\cong\triangle DEM,DE = BD = BE = 2,\angle DEM = 60^{\circ},\therefore\angle MDE=\angle NDB = 90^{\circ},CE = BC - BE = 5.\therefore ME=\frac{DE}{\cos60^{\circ}}=\frac{2}{\frac{1}{2}}=4.\therefore CM = ME + CE = 9$.综上所述,$CM$的长是$6$或$8$或$9$.
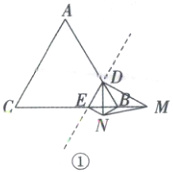
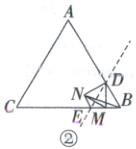

12.6或8或9 解析:过点$D$作$DE// AC$,交$BC$于点$E$.当$\angle DBN = 90^{\circ}$且点$M$在$CB$的延长线上时,如图①$\because\triangle ABC$是等边三角形,$DE// AC,\therefore$易得$\triangle BDE$是等边三角形.$\therefore DE = DB = 2,\angle BDE = 60^{\circ}.\because\triangle DMN$是等边三角形,$\therefore DN = DM,\angle NDM = 60^{\circ}.\therefore\angle BDE=\angle NDM.\therefore$易得$\angle EDN=\angle BDM.\therefore\triangle DEN\cong\triangle DBM.\therefore\angle DEN=\angle DBM = 180^{\circ}-60^{\circ}=120^{\circ},EN = BM.\because$易得$\angle DEB=\angle DBE = 60^{\circ},\therefore\angle BEN=\angle DEN-\angle DEB = 60^{\circ},\angle NBE=\angle DBN-\angle DBE = 30^{\circ}.\therefore\angle BNE = 90^{\circ}.\therefore EN=\frac{1}{2}BE = 1.\therefore BM = 1.\therefore MC = BC + BM = 7 + 1 = 8$.当$\angle BDN = 90^{\circ}$且点$M$在$BC$上时,如图②.同理可得$\triangle DEN\cong\triangle DBM,\angle NDE=\angle BDN-\angle BDE = 90^{\circ}-60^{\circ}=30^{\circ},\therefore\angle NED=\angle MBD = 60^{\circ},\angle DMB=\angle DNE = 90^{\circ}.\therefore BM = BD·\cos60^{\circ}=2×\frac{1}{2}=1.\therefore CM = BC - BM = 6$.当$\angle BND = 90^{\circ}$且点$M$在$CB$上时,如图③.同理可证$\triangle DBN\cong\triangle DEM,DE = BD = 2,\angle DEM = 60^{\circ}$,$\therefore\angle DME=\angle DNB = 90^{\circ}.\therefore ME = DE·\cos60^{\circ}=2×\frac{1}{2}=1.\therefore BM = 1.\therefore CM = BC - BM = 6$.当$\angle BND = 90^{\circ}$且点$M$在$CB$的延长线上时,如图④.同理可证$\triangle DBN\cong\triangle DEM,DE = BD = BE = 2,\angle DEM = 60^{\circ},\therefore\angle MDE=\angle NDB = 90^{\circ},CE = BC - BE = 5.\therefore ME=\frac{DE}{\cos60^{\circ}}=\frac{2}{\frac{1}{2}}=4.\therefore CM = ME + CE = 9$.综上所述,$CM$的长是$6$或$8$或$9$.



查看更多完整答案,请扫码查看


