《2026年通城学典全国中考试题分类精粹中考数学》

31. (2025·龙东地区)若圆锥的底面半径为3，高为4，则圆锥侧面展开图的面积为15π。

答案： 31.15π

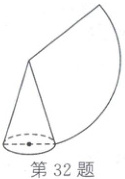
32. (2025·达州)如图，圆锥的侧面展开图是一个扇形。已知圆锥的底面半径为2，则扇形的弧长是4π。

答案： 32.4π

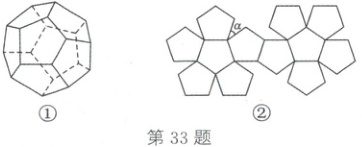
33. (2025·长春)如图①所示为一个正十二面体，它的每个面都是正五边形，如图②所示为其表面展开图，则$\angle\alpha=$36°。

答案： 33.36°

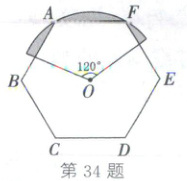
34. (2025·烟台)如图，正六边形ABCDEF的边长为4，中心为点O，以点O为圆心，AB长为半径作圆心角为$120^{\circ}$的扇形，则图中涂色部分的面积为$\frac{16π}{3}-8\sqrt{3}$。

答案：
34.$\frac{16π}{3}-8\sqrt{3}$ 解析：如图，连接OA,OE,OF，过点O作OM⊥AF于点M.
∵六边形ABCDEF为正六边形，
∴OA = OE = OF，∠AOF = ∠EOF = $\frac{360°}{6}$ = 60°，∠BAF = 120°.
∴△OAF和△OEF均为等边三角形，∠AOE = ∠AOF + ∠EOF = 60° + 60° = 120°.
∴∠OEF = ∠OAF = 60°，OA = OF = AF = AB = 4，S△AOF = S△EOF.
∴点A,F在该扇形上.
∵OM⊥AF，
∴AM = FM = $\frac{1}{2}$AF = 2.
∴OM = $\sqrt{OA^{2}-AM^{2}}$ = $\sqrt{4^{2}-2^{2}}$ = 2$\sqrt{3}$.
∴S△OAF = $\frac{1}{2}$AF·OM = $\frac{1}{2}$×4×2$\sqrt{3}$ = 4$\sqrt{3}$.
∵∠BAF = 120°，
∴∠OAG = ∠BAF - ∠OAF = 120° - 60° = 60°.
∴∠OAG = ∠OEH.
∵∠GOH = ∠AOE = 120°，即∠GOA + ∠AOH = ∠AOH + ∠HOE = 120°，
∴∠GOA = ∠HOE.又
∵OA = OE，
∴△GOA≌△HOE.
∴S△GOA = S△HOE.
∴S△GOA + S四边形AOHF = S△HOE + S四边形AOHF.
∴S五边形AGOHF = S四边形AOEF = 2S△AOF = 8$\sqrt{3}$.
∴S涂色 = S扇形 - S五边形AGOHF = $\frac{120π×4^{2}}{360}$ - 8$\sqrt{3}$ = $\frac{16π}{3}$ - 8$\sqrt{3}$.
　　　　　　　

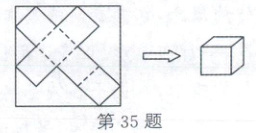
35. (2025·威海)如图，小明同学将正方形硬纸板沿实线剪开，得到一个立方体的表面展开图。若正方形硬纸板的边长为12 cm，则折成立方体的棱长为$\frac{12\sqrt{2}}{5}$cm。

答案： 35.$\frac{12\sqrt{2}}{5}$

36. (2025·南京)将如图①所示的纸杯侧面展开，得到以点O为圆心的扇环ABCD。
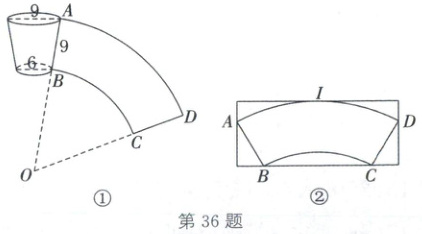
(1)求OB及$\overset{\frown}{AD}$的长。
(2)设矩形纸片的长和宽分别为b，a($a\leqslant b$)。
①如图②，将扇环ABCD放于矩形纸片之上，矩形一边与$\overset{\frown}{AD}$所在圆相切于点I，点A，B，C，D均在矩形的边上，直接写出a，b的值。
②一矩形纸片的宽为18.2，长为25.7，能否剪出上述的扇环ABCD(参考数据：$\sqrt{3}\approx1.732$)？
③一矩形纸片的规格为$15× b$，当该纸片能剪出扇环ABCD时，求b的取值范围(提示：$\sin^{2}\alpha+\cos^{2}\alpha = 1$，$\sin(\alpha - \beta)=\sin\alpha\cos\beta - \cos\alpha\sin\beta$)。

答案：
36.（1）设∠O = n°.由题图①，知$\overset{\frown}{AD}$ = 9π，$\overset{\frown}{BC}$ = 6π.
∴$\frac{nπ}{180}$·OB = 6π，$\frac{nπ}{180}$·(OB + 9) = 9π.
∴$\frac{OB}{OB + 9}$ = $\frac{2}{3}$.
∴OB = 18.（2）①如图①，延长AB,DC交于点O，连接IO交BC于点H.
∵四边形EFKG为矩形，
∴EF//GK，∠G = ∠K = 90°.
∵矩形的一边与AD所在圆（即⊙O）相切于点I，OI为⊙O的半径，
∴OI⊥EF.
∵EF//GK，
∴OI⊥GK.由（1），得OB = OC = 18，AB = CD = 9，BC = 6π，
∴OA = OI = 9 + 18 = 27.
∴∠BOC = $\frac{6π}{2×18π}$×360° = 60°.
∴△OBC是等边三角形.
∴BC = OB = 18，∠OBC = ∠OCB = 60°.
∴∠ABG = 60°.
∴∠BAG = 30°.
∴BG = $\frac{1}{2}$AB = $\frac{9}{2}$.同理可得CK = $\frac{9}{2}$.
∴GK = $\frac{9}{2}$ + 18 + $\frac{9}{2}$ = 27，即b = 27.易得OH = 9$\sqrt{3}$，
∴IH = OI - OH = 27 - 9$\sqrt{3}$，即a = 27 - 9$\sqrt{3}$.②将扇环按如图②所示的方式放置时，过点C作CF⊥AO于点F，过点D作DE⊥AO于点E，连接BC，延长AB,DC交于点O.由（1）（2），得OB = OC = 18，∠O = 60°，△OBC是等边三角形，
∴在Rt△BCF中，∠OBC = 60°，∠CFB = 90°，BC = OB = 18.易得BF = 9，CF = 9$\sqrt{3}$.在Rt△ODE中，∠OED = 90°，OD = OA = 27，∠O = 60°.易得OE = $\frac{27}{2}$，DE = $\frac{27}{2}$$\sqrt{3}$≈23.382＜25.7.
∵AB = 9，BF = 9，
∴AF = AB + BF = 9 + 9 = 18＜18.2.
∴宽为18.2，长为25.7的矩形纸片，能剪出上述的扇环ABCD.③如图③，延长AB,DC交于点O.当AD在MN上滚动，且点A在NQ上，点D在NS上，点C在SQ上时，MN最小，即b最小.此时，P为AD所在圆（即⊙O）与矩形的边MN的切点，连接OP，交SQ于点H，交BC于点G，则易得OP⊥MN，OP⊥SQ，PH = 15，PG = 9，OG = 18.
∴GH = PH - PG = 15 - 9 = 6，OH = OG - GH = 18 - 6 = 12.过点D作DJ⊥OP于点J，过点A作AK⊥OP于点K.设∠COG = β(0°＜β≤60°)，∠GOB = α(0°＜α≤60°).
∴在Rt△OCH中，cosβ = $\frac{OH}{OC}$ = $\frac{12}{18}$ = $\frac{2}{3}$.
∴sinβ = $\sqrt{1 - (\frac{2}{3})^{2}}$ = $\frac{\sqrt{5}}{3}$，易得DS = DC·cosβ = 6.
∴DS = GH.此时点J与点G重合.
∴在Rt△ODJ中，DJ = OD·sinβ = 27×$\frac{\sqrt{5}}{3}$ = 9$\sqrt{5}$.
∵∠BOC = 60°，
∴α = 60° - β.
∴sinα = sin(60° - β) = sin60°cosβ - cos60°sinβ = $\frac{2\sqrt{3}-\sqrt{5}}{6}$.在Rt△AOK中，AK = OA·sinα = 27×$\frac{2\sqrt{3}-\sqrt{5}}{6}$ = 9$\sqrt{3}$ - $\frac{9}{2}$$\sqrt{5}$.
∴易得MN = AK + DJ = 9$\sqrt{3}$ + $\frac{9}{2}$$\sqrt{5}$.
∴b≥9$\sqrt{3}$ + $\frac{9}{2}$$\sqrt{5}$.