《2026年通城学典全国中考试题分类精粹中考数学》

10. (2025·内江)2025 年春节期间，我国国产动画电影《哪吒之魔童闹海》刷新了中国电影票房的新纪录，商家推出 $ A $，$ B $ 两款“哪吒”文旅纪念品。已知购进 $ A $ 款 $ 200 $ 个，$ B $ 款 $ 300 $ 个，需花费 $ 14000 $ 元；购进 $ A $ 款 $ 100 $ 个，$ B $ 款 $ 200 $ 个，需花费 $ 8000 $ 元。
(1) $ A $，$ B $ 两款“哪吒”纪念品每个的进价分别为多少元？
(2) 根据网上预约的情况，如果该商家计划用不超过 $ 12000 $ 元的资金购进 $ A $，$ B $ 两款“哪吒”纪念品共 $ 400 $ 个，那么至少需要购进 $ B $ 款“哪吒”纪念品多少个？
(3) 在销售中，该商家发现当每个 $ A $ 款“哪吒”纪念品的售价为 $ 60 $ 元时，可售出 $ 200 $ 个，售价每增加 $ 1 $ 元，销售量将减少 $ 5 $ 个。设每个 $ A $ 款“哪吒”纪念品的售价为 $ a(60 \leq a \leq 100) $ 元，该商家销售 $ A $ 款“哪吒”纪念品的利润为 $ W $ 元，求 $ W $ 关于 $ a $ 的函数解析式，并求出 $ W $ 的最大值。

答案： 10.
(1)设每个A款“哪吒”纪念品的进价为x元，每个B款“哪吒”纪念品的进价为y元.由题意，得$\begin{cases}200x + 300y = 14000\\100x + 200y = 8000\end{cases}$，解得$\begin{cases}x = 40\\y = 20\end{cases}$.
∴每个A款“哪吒”纪念品的进价为40元，每个B款“哪吒”纪念品的进价为20元
(2)设需要购进B款“哪吒”纪念品m个，则需要购进A款“哪吒”纪念品(400 - m)个.由题意，得40(400 - m) + 20m ≤ 12000，解得m ≥ 200.
∴m的最小值为200.
∴至少需要购进B款“哪吒”纪念品200个
(3)由题意，得W = (a - 40)[200 - 5(a - 60)] = (a - 40)(200 - 5a + 300) = (a - 40)(500 - 5a) = 500a - 20000 - 5a² + 200a = -5(a - 70)² + 4500.
∵ - 5 ＜ 0，60 ≤ a ≤ 100，
∴当a = 70时，W最大，最大值为4500

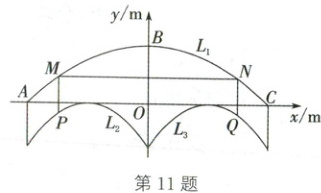
11. (2025·陕西)某景区大门上半部分的截面示意图如图所示，顶部 $ L_{1} $，左、右门洞 $ L_{2} $，$ L_{3} $ 均呈抛物线型，水平横梁 $ AC = 16m $，$ L_{1} $ 的最高点 $ B $ 到 $ AC $ 的距离 $ BO = 4m $，$ L_{2} $，$ L_{3} $ 关于 $ BO $ 所在直线对称。$ MN $，$ MP $，$ NQ $ 为框架，点 $ M $，$ N $ 在 $ L_{1} $ 上，点 $ P $，$ Q $ 分别在 $ L_{2} $，$ L_{3} $ 上，$ MN // AC $，$ MP \perp AC $，$ NQ \perp AC $。以 $ O $ 为原点，$ AC $ 所在直线为 $ x $ 轴，$ BO $ 所在直线为 $ y $ 轴，建立平面直角坐标系。
(1) 求抛物线 $ L_{1} $ 对应的函数解析式；
(2) 已知抛物线 $ L_{3} $ 对应的函数解析式为 $ y = -\frac{3}{16}(x - 4)^{2} $，$ NQ = \frac{5}{2}m $，求 $ MN $ 的长。

答案： 11.
(1)
∵BO = 4m，
∴抛物线L₁的顶点B的坐标为(0, 4).设抛物线L₁对应的函数解析式为y = ax² + 4.
∵AC = 16 m，
∴由抛物线的对称性，得A(-8, 0)，C(8, 0).将C(8, 0)代入y = ax² + 4，得a = -$\frac{1}{16}$.
∴抛物线L₁对应的函数解析式为y = -$\frac{1}{16}$x² + 4
(2)由
(1)，得抛物线L₁对应的函数解析式为y = -$\frac{1}{16}$x² + 4，又
∵MN//AC，MP⊥AC，NQ⊥AC，NQ = $\frac{5}{2}$m，且抛物线L₃对应的函数解析式为y = -$\frac{3}{16}$(x - 4)²，
∴$y_N - y_Q$ = -$\frac{1}{16}$x² + 4 - [-$\frac{3}{16}$(x - 4)²] = $\frac{5}{2}$.整理，得(x - 6)² = 0.解得x₁ = x₂ = 6.由抛物线的对称性，得MN = 2×6 = 12(m)

12. (2025·南充)学校计划租用客车送师生到某红色基地，参加主题为“缅怀先烈，强国有我”的研学活动，请阅读下列材料，并完成相关问题。


(1) $ A $，$ B $ 两种型号的客车每辆载客量分别是多少？
(2) 本次研学活动学校的最少租车费用是多少？

答案： 12.
(1)设A型客车每辆载客量为x人，则B型客车每辆载客量为(x - 15)人.根据题意，得$\frac{600}{x}$ = $\frac{450}{x - 15}$，解得x = 60.经检验，x = 60是所列方程的解，且符合题意.
∴x - 15 = 60 - 15 = 45.
∴A型客车每辆载客量为60人，B型客车每辆载客量为45人
(2)
∵租用A型客车m辆，
∴租用B型客车(10 - m)辆.根据题意，得60m + 45(10 - m) ≥ 530，解得m ≥ $\frac{16}{3}$.设本次研学活动学校的租车总费用为w元，则w = (3200 - 50m)m + 3000×0.8(10 - m) = -50m² + 800m + 24000.
∵ - 50 ＜ 0，且抛物线的对称轴为直线m = -$\frac{800}{2×(-50)}$ = 8，
∴当m ≤ 8时，w随m的增大而增大.
∵m取正整数，且m ≥ $\frac{16}{3}$，
∴当m = 6时，w取得最小值，最小值为 - 50×6² + 800×6 + 24000 = 27000.
∴本次研学活动学校的最少租车费用是27000元