《2026年通城学典全国中考试题分类精粹中考数学》

24. (2025·眉山)解方程：$2(x - 1) = 2 + x$.

答案： 24.$x = 4$

25. 解方程组：
(1) (2025·新疆)$\begin{cases}3x - y = 5,\\x + y = 3\end{cases}$
(2) (2025·山西)$\begin{cases}3x - 2y = 11,\\x + 2y = 1\end{cases}$

答案： 25.
(1)$\begin{cases}x = 2, \\y = 1 \end{cases}$
(2)$\begin{cases}x = 3, \\y = - 1 \end{cases}$

26. (2025·河北)一般固体都具有热胀冷缩的性质，固体受热后其长度的增加称为线膨胀. 在$0\sim100^{\circ}C$（本题涉及的温度均在此范围内），原长为$l$m的铜棒、铁棒受热后，伸长量$y$（m）与温度的增加量$x$（$^{\circ}C$）之间的关系均为$y = \alpha lx$，其中$\alpha$为常数，称为该金属的线膨胀系数. 已知铜的线膨胀系数$\alpha_{Cu} = 1.7×10^{-5}/^{\circ}C$，原长为$2.5$m的铁棒从$20^{\circ}C$加热到$80^{\circ}C$伸长了$1.8×10^{-3}$m.
(1) 原长为$0.6$m的铜棒受热后升高$50^{\circ}C$，求该铜棒的伸长量（用科学记数法表示）.
(2) 求铁的线膨胀系数$\alpha_{Fe}$. 若原长为$1$m的铁棒受热后伸长$4.8×10^{-4}$m，求该铁棒温度的增加量.
(3) 将原长相等的铜棒和铁棒从$0^{\circ}C$开始分别加热，当它们的伸长量相同时，若铁棒的温度比铜棒的温度高$20^{\circ}C$，求该铁棒温度的增加量.

答案： 26.
(1)$1.7 × 10^{- 5} × 0.6 × 50 = 5.1 × 10^{- 4}(m)$,即该铜棒的伸长量为$5.1 × 10^{- 4}m$
(2)$\alpha_{Fe} = \frac{1.8 × 10^{- 3}}{2.5 × (80 - 20)} = 1.2 × 10^{- 5}/^{\circ}C$.$4.8 × 10^{- 4} ÷ (1.2 × 10^{- 5} × 1) = 40(^{\circ}C)$,即该铁棒温度的增加量为$40^{\circ}C$
(3)设铜棒增加的温度为$x^{\circ}C$,则铁棒增加的温度为$(x + 20)^{\circ}C$,它们的原长均为$lm$.由题意,得$1.7 × 10^{- 5} × l × x = 1.2 × 10^{- 5} × l × (x + 20)$,整理,得$17x = 12x + 240$,解得$x = 48$.$\therefore x + 20 = 48 + 20 = 68$,即该铁棒温度的增加量为$68^{\circ}C$

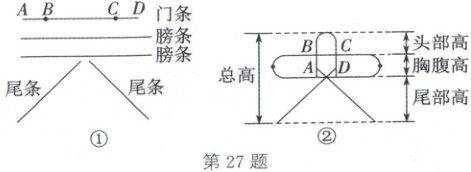
27. (2025·北京)北京风筝制作技艺是国家级非物质文化遗产. 为制作一只京燕风筝，小明准备了五根直竹条（如图①）：一根门条、两根等长的膀条和两根等长的尾条. 他将门条和膀条分别烤弯后与尾条一起扎成风筝的骨架（如图②），其头部高、胸腹高与尾部高的比是$1:1:2$. 已知单根膀条长是胸腹高的$5$倍，门条比膀条短$10$cm，图①中$BC$的长是门条长的$\frac{5}{9}$，$AB$，$CD$的长均等于胸腹高. 求这只风筝的骨架的总高.

答案： 27.设胸腹高为$xcm$,则$AB = CD = xcm$,单根膀条长为$5xcm\therefore$门条$AD$的长为$(5x - 10)cm.\therefore BC = \frac{5}{9}(5x - 10)cm.\because$头部高、胸腹高与尾部高的比为$1:1:2,\therefore$头部高为$xcm$,尾部高为$2xcm$,这只风筝的骨架的总高为$4xcm$ $\because AD = AB + BC + CD$,$\therefore 5x - 10 = x + \frac{5}{9}(5x - 10) + x$, 解得$x = 20.\therefore 4x = 80.\therefore$这只风筝的骨架的总高为$80cm$