《2026年通城学典全国中考试题分类精粹中考数学》

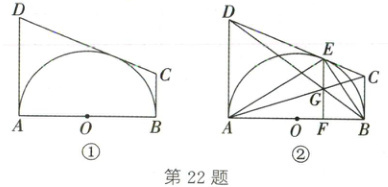
22. (2025·长沙)如图①，点$O$是以$AB$为直径的半圆的圆心，$AD$与$BC$均为该半圆的切线，$C$，$D$均为直径$AB$上方的动点，连接$CD$，且始终满足$CD = AD + BC$。
(1) 求证：$CD$与该半圆相切。
(2) 当半径$r = \sqrt{2}$时，令$AD = a$，$BC = b$，$m=\frac{2}{2 + a}+\frac{2}{2 + b}$，$n=\frac{a}{1 + a}+\frac{b}{1 + b}$，比较$m$与$n$的大小，并说明理由。
(3) 在(1)的条件下，如图②，当半径$r = 1$时，若$E$为$CD$与该半圆的切点，$AC$与$BD$交于点$G$，连接$EG$并延长，交$AB$于点$F$，连接$AE$，$BE$。令$EG = x$，$\frac{4}{AE· BE}+\frac{1}{FG}+CD = y$，求$y$关于$x$的函数解析式（不考虑自变量$x$的取值范围）。

答案：
22.
(1)如图①，连接$CO$并延长，交$DA$的延长线于点$M$，过点$O$作$OE\perp CD$于点$E$。$\because AD$与$BC$均为该半圆的切线，$\therefore AD\perp AB$，$BC\perp AB$。$\therefore AD// BC$。$\therefore\angle M = \angle OCB$。$\because O$为$AB$的中点，$\therefore OA = OB$。在$\triangle OAM$和$\triangle OBC$中，$\begin{cases}\angle M = \angle OCB\\\angle OAM = \angle OBC = 90^{\circ}\\OA = OB\end{cases}$，$\therefore\triangle OAM\cong\triangle OBC$。$\therefore AM = BC$。
$\because CD = AD + BC$，$\therefore CD = AD + AM = DM$。$\therefore\angle M = \angle OCE$。$\therefore\angle OCB = \angle OCE$，即$CO$平分$\angle BCD$。又$\because OE\perp CD$，$OB\perp CB$，$\therefore OE = OB$。$\therefore CD$与该半圆相切。
(2)$m = n$ 理由：如图②，过点$C$作$CM\perp AD$于点$M$。易得四边形$AMCB$是矩形，$\therefore AB = MC$，$AM = BC$。在$Rt\triangle CDM$中，由勾股定理，得$CD^{2}=DM^{2}+CM^{2}$。$\because CD = AD + BC = a + b$，$DM=\vert a - b\vert$，$CM = 2r$，$\therefore(a + b)^{2}=(a - b)^{2}+4r^{2}$。
$\therefore r^{2}=AD· BC = ab = 4$。$m=\frac{2}{2 + a}+\frac{2}{2 + b}=\frac{ab}{ab + a}+\frac{ab}{ab + b}=\frac{b}{1 + b}+\frac{a}{1 + a}=n$。
(3)$\because CD$，$AD$，$BC$均为该半圆的切线，$\therefore DA = DE$，$CB = CE$。$\because AD\perp AB$，$BC\perp AB$，$\therefore AD// BC$。$\therefore\triangle DAG\sim\triangle BCG$。$\therefore\frac{CG}{GA}=\frac{CB}{AD}=\frac{CE}{ED}$。$\therefore\frac{CG}{CA}=\frac{CE}{CD}$。$\because\angle ACD = \angle GCE$，$\therefore\triangle ACD\sim\triangle GCE$。$\therefore\angle ADC = \angle GEC$。$\therefore EG// AD// BC$，$FG// AD// BC$。$\therefore\frac{FG}{BC}=\frac{AF}{AB}$，$\frac{FG}{AD}=\frac{BF}{AB}$。$\therefore\frac{FG}{BC}+\frac{FG}{AD}=1$。$\therefore\frac{1}{BC}+\frac{1}{AD}=\frac{1}{FG}$。同理，可得$\frac{1}{BC}+\frac{1}{AD}=\frac{1}{EG}$。$\therefore FG = EG = x$。由
(2)可知，$r^{2}=AD· BC = DE· EC = 1$。$\therefore\frac{1}{DE}+\frac{1}{CE}=\frac{1}{BC}+\frac{1}{AD}=\frac{1}{EG}=\frac{DE + CE}{DE· CE}=\frac{DC}{1}=\frac{1}{x}$。易知在$Rt\triangle ABE$中，$\because\frac{1}{2}AE· BE=\frac{1}{2}·2x·2r = 2x$，$\therefore AE· BE = 4x$。
$\therefore\frac{4}{AE· BE}=\frac{4}{4x}=\frac{1}{x}$。$\therefore y=\frac{4}{AE· BE}+\frac{1}{FG}+DC=\frac{1}{x}+\frac{1}{x}+\frac{1}{x}=\frac{3}{x}$

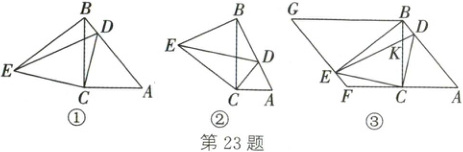
23. (2025·湖北)在$\triangle ABC$中，$\angle ACB = 90^{\circ}$，将$\triangle ABC$绕点$C$旋转得到$\triangle DEC$，点$A$的对应点$D$落在边$AB$上，连接$BE$。
(1) 如图①，求证：$\triangle BCE\sim\triangle ACD$。
(2) 如图②，当$BC = 2$，$AC = 1$时，求$BE$的长。
(3) 如图③，过点$E$作$AB$的平行线，交$AC$的延长线于点$F$，过点$B$作$AC$的平行线，交$EF$于点$G$，$DE$与$BC$交于点$K$。
① 求证：$AC = CF$；
② 当$\frac{GF}{GB}=\frac{5}{6}$时，直接写出$\frac{KD}{KE}$的值。

答案： 23.
(1)$\because$将$\triangle ABC$绕点$C$旋转得到$\triangle DEC$，点$A$的对应点$D$落在边$AB$上，$\therefore AC = CD$，$CB = CE$，$\angle ACD = \angle BCE$。$\because\frac{AC}{CB}=\frac{CD}{CE}$，$\therefore\triangle BCE\sim\triangle ACD$。
(2)$\because BC = 2$，$AC = 1$，$\angle ACB = 90^{\circ}$，$\therefore AC = CD = 1$，$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{5}$。$\therefore\tan A=\frac{BC}{AC}=2$。过点$D$作$DH\perp AC$于点$H$，则$\tan A=\frac{DH}{AH}=2$。$\therefore DH = 2AH$。在$Rt\triangle CDH$中，$CH^{2}+DH^{2}=CD^{2}$，即$(1 - AH)^{2}+(2AH)^{2}=1^{2}$，解得$AH=\frac{2}{5}$或$AH = 0$（舍去）。$\therefore DH=\frac{4}{5}$。在$Rt\triangle ADH$中，$AH^{2}+DH^{2}=AD^{2}$，$\therefore AD=\sqrt{AH^{2}+(2AH)^{2}}=\sqrt{5}AH=\frac{2\sqrt{5}}{5}$。
$\because\triangle BCE\sim\triangle ACD$，$\therefore\frac{BE}{AD}=\frac{BC}{AC}$，即$\frac{BE}{2\sqrt{5}}=\frac{2}{1}$。$\therefore BE=\frac{4\sqrt{5}}{5}$。
(3)①设旋转角为$\alpha$，则$\angle ACD = \angle BCE = \alpha$，$AC = CD$，$CB = CE$，$\therefore\angle CDA = \angle A=\frac{180^{\circ}-\alpha}{2}=90^{\circ}-\frac{1}{2}\alpha$，$\angle CEB = \angle CBE=\frac{180^{\circ}-\alpha}{2}=90^{\circ}-\frac{1}{2}\alpha$。$\because\angle ACB = 90^{\circ}$，$\therefore\angle BCF = 90^{\circ}$，$\angle DCB = 90^{\circ}-\alpha$。$\angle ECF = 90^{\circ}-\alpha$。$\therefore\angle DCB = \angle ECF$。
$\because GF// AB$，$\therefore\angle F + \angle A = 180^{\circ}$。$\because\angle CDA + \angle CDB = 180^{\circ}$，$\angle CDA = \angle A$，$\therefore\angle CDB = \angle F$。$\because\angle DCB = \angle ECF$，$\angle CDB = \angle F$，$CB = CE$，$\therefore\triangle BCD\cong\triangle ECF$。$\therefore CD = CF$。$\because CD = AC$，$\therefore AC = CF$。②$\because\frac{GF}{GB}=\frac{5}{6}$，$\therefore$设$GF = 5k$，$GB = 6k$。$\because GF// AB$，$BG// AF$，$\therefore$四边形$ABGF$是平行四边形。$\therefore AB = GF = 5k$，$AF = BG = 6k$，$\angle G = \angle A$。由①，得$CD = AC = CF = 3k$。在$Rt\triangle ABC$中，$AB^{2}=BC^{2}+AC^{2}$，$\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{(5k)^{2}-(3k)^{2}}=4k$。$\therefore\sin A=\frac{BC}{AB}=\frac{4k}{5k}=\frac{4}{5}$。$\therefore\sin G = \sin A=\frac{4}{5}$。由旋转的性质，可得$CE = CB$，$\therefore\angle CEB = \angle CBE$。$\because\triangle CBD\cong\triangle CEF$，$\therefore\angle CBD = \angle CEF$。$\because GF// AB$，$\therefore\angle FEB + \angle ABE = 180^{\circ}$，即$\angle CEF + \angle CEB + \angle CBE + \angle CBD = 180^{\circ}$，即$2(\angle CEF + \angle CEB)=2\angle FEB = 180^{\circ}$。$\therefore\angle FEB = 90^{\circ}$。$\therefore\angle BEG = 90^{\circ}$。$\therefore\sin G=\frac{BE}{BG}=\frac{4}{5}$，即$\frac{BE}{6k}=\frac{4}{5}$。$\therefore BE=\frac{24}{5}k$。由①，得$\angle ADC = \angle CEB = 90^{\circ}-\frac{1}{2}\alpha$，$\angle ADC + \angle CDB = 180^{\circ}$，$\therefore\angle CEB + \angle CDB = 180^{\circ}$。$\therefore C$，$D$，$B$，$E$四点共圆。$\therefore\angle BED = \angle BCD$。$\because\angle BEK = \angle KCD$，$\angle BKE = \angle DKC$，$\therefore\triangle BEK\sim\triangle DCK$。$\therefore\frac{DK}{BK}=\frac{CK}{EK}=\frac{CD}{EB}=\frac{3k}{\frac{24}{5}k}=\frac{5}{8}$。设$DK = 5x$，$BK = 8x$，$CK = 5y$，$EK = 8y$，则$BC = BK + CK = 8x + 5y = 4k$①。由旋转的性质，可得$DE = AB = 5k$，$\therefore DE = DK + EK = 5x + 8y = 5k$②。联立①②，可得$x=\frac{7}{39}k$，$y=\frac{20}{39}k$，$\therefore\frac{KD}{KE}=\frac{5x}{8y}=\frac{5×\frac{7}{39}k}{8×\frac{20}{39}k}=\frac{7}{32}$。