第123页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
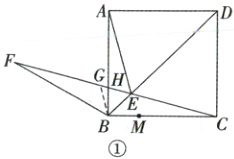
36. (2025·遂宁)如图,在边长为1的正方形ABCD的对角线BD上取一点E,使∠BAE=15°,连接CE并延长至点F,连接BF,使BF=BC,CF与AB相交于点H。有下列结论:① AE=CE;② BE + AE = EF;③ $\frac{AH}{BH}$ = 2√3 - 1;④ M是边BC上一动点,连接HM,将△BHM沿HM翻折,点B落在点P处,连接BP交HM于点Q,连接DQ,则DQ长的最小值为$\frac{\sqrt{7} + \sqrt{3} - 2}{2}$。其中,正确的是

①②④
(填序号)。
答案:
36.①②④ 解析:$\because$四边形$ABCD$是正方形,$E$是正方形$ABCD$的对角线$BD$上的点,$\therefore AD=CD$,$\angle ADE=\angle CDE$。
又$\because DE=DE$,$\therefore \triangle ADE\cong\triangle CDE$,$\therefore AE=CE$。故①正确。
如图①,在$FC$上取一点$G$,使得$BG=BE$。
$\because$四边形$ABCD$是正方形,$BD$是对角线,$\therefore \angle ADE=\angle CBD=45^{\circ}$,$\angle BAD=\angle BCD=90^{\circ}$,$AD=CD$。
$\because \angle BAE=15^{\circ}$,$\therefore \angle DAE=90^{\circ}-15^{\circ}=75^{\circ}$,$\therefore \angle AED=180^{\circ}-45^{\circ}-75^{\circ}=60^{\circ}$。
$\because \triangle ADE\cong\triangle CDE$,$\therefore \angle AED=\angle CED=60^{\circ}$,$\angle DAE=\angle DCE=75^{\circ}$。
$\therefore \angle HEB=\angle CED=60^{\circ}$,$\angle BCE=90^{\circ}-75^{\circ}=15^{\circ}$,$\therefore \triangle GEB$是等边三角形,$\therefore \angle EBG=60^{\circ}$,$EG=BE$。
又$\because BF=BC$,$\therefore \angle F=\angle BCF=15^{\circ}$,$\therefore \angle FBC=180^{\circ}-15^{\circ}-15^{\circ}=150^{\circ}$。
$\therefore \angle FBG=\angle FBC-\angle GBE-\angle CBE=150^{\circ}-60^{\circ}-45^{\circ}=45^{\circ}=\angle CBE$。
$\because \angle F=\angle BCF$,$BF=BC$,$\therefore \triangle FBG\cong\triangle CBE$,$\therefore FG=CE$。
$\therefore EF=EG+FG=BE+CE=BE+AE$,即$BE + AE=EF$。故②正确。
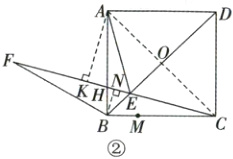
如图②,连接$AC$交$BD$于点$O$,则$\angle DAO=\angle ACB=45^{\circ}$,过点$A$,$B$分别作$FC$的垂线,垂足分别为$K$,$N$。
$\because AB=1$,$\therefore$易得$AO=BO=\frac{\sqrt{2}}{2}AB=\frac{\sqrt{2}}{2}$,$AC=\sqrt{2}AB=\sqrt{2}$。
$\because \angle DAE=75^{\circ}$,$\angle DAO=45^{\circ}$,$\therefore \angle EAO=30^{\circ}$。
$\because$在正方形$ABCD$中,$AC\perp BD$,$\therefore EO=AO·\tan\angle EAO=\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{3}=\frac{\sqrt{6}}{6}$,$\therefore BE=OB - OE=\frac{\sqrt{2}}{2}-\frac{\sqrt{6}}{6}$。
$\because \angle BCE=15^{\circ}$,$\angle ACB=45^{\circ}$,$\therefore \angle ACK=30^{\circ}$,$\therefore AK=\frac{1}{2}AC=\frac{\sqrt{2}}{2}$。
在$Rt\triangle BEN$中,$BN=BE·\sin\angle NEB=BE·\sin60^{\circ}=(\frac{\sqrt{2}}{2}-\frac{\sqrt{6}}{6})×\frac{\sqrt{3}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$。
$\because AK\perp FC$,$BN\perp FC$,$\therefore KA// BN$,$\therefore \triangle AHK\sim\triangle BHN$,$\therefore \frac{AH}{BH}=\frac{AK}{BN}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}-\sqrt{2}}{4}}=\sqrt{3}+1$。故③错误。
$\because AB=AH + BH=1$,$\frac{AH}{BH}=\sqrt{3}+1$,$\therefore (\sqrt{3}+1)· BH + BH=1$,即$BH=\frac{1}{\sqrt{3}+2}=2-\sqrt{3}$。
如图③,$\because M$是边$BC$上一动点,将$\triangle BHM$沿$HM$翻折,点$B$落在点$P$处,$\therefore PQ\perp HM$,$\therefore \angle HQB=90^{\circ}$,$\therefore$点$Q$在以$HB$为直径的圆上运动。
取$HB$的中点$T$,连接$DT$,$\therefore$当点$Q$在$DT$上时,$DQ$的长取得最小值,最小值为$DT - BT$的值。
$\because BT=\frac{1}{2}BH=\frac{1}{2}(2 - \sqrt{3})=1-\frac{\sqrt{3}}{2}$,$\therefore AT=AB - BT=\frac{\sqrt{3}}{2}$。
$\therefore DT=\sqrt{AD^{2}+AT^{2}}=\sqrt{1+(\frac{\sqrt{3}}{2})^{2}}=\frac{\sqrt{7}}{2}$,$\therefore DT - BT=\frac{\sqrt{7}}{2}-(1-\frac{\sqrt{3}}{2})=\frac{\sqrt{7}+\sqrt{3}-2}{2}$。故④正确。
综上所述,正确的是①②④。

36.①②④ 解析:$\because$四边形$ABCD$是正方形,$E$是正方形$ABCD$的对角线$BD$上的点,$\therefore AD=CD$,$\angle ADE=\angle CDE$。
又$\because DE=DE$,$\therefore \triangle ADE\cong\triangle CDE$,$\therefore AE=CE$。故①正确。
如图①,在$FC$上取一点$G$,使得$BG=BE$。
$\because$四边形$ABCD$是正方形,$BD$是对角线,$\therefore \angle ADE=\angle CBD=45^{\circ}$,$\angle BAD=\angle BCD=90^{\circ}$,$AD=CD$。
$\because \angle BAE=15^{\circ}$,$\therefore \angle DAE=90^{\circ}-15^{\circ}=75^{\circ}$,$\therefore \angle AED=180^{\circ}-45^{\circ}-75^{\circ}=60^{\circ}$。
$\because \triangle ADE\cong\triangle CDE$,$\therefore \angle AED=\angle CED=60^{\circ}$,$\angle DAE=\angle DCE=75^{\circ}$。
$\therefore \angle HEB=\angle CED=60^{\circ}$,$\angle BCE=90^{\circ}-75^{\circ}=15^{\circ}$,$\therefore \triangle GEB$是等边三角形,$\therefore \angle EBG=60^{\circ}$,$EG=BE$。
又$\because BF=BC$,$\therefore \angle F=\angle BCF=15^{\circ}$,$\therefore \angle FBC=180^{\circ}-15^{\circ}-15^{\circ}=150^{\circ}$。
$\therefore \angle FBG=\angle FBC-\angle GBE-\angle CBE=150^{\circ}-60^{\circ}-45^{\circ}=45^{\circ}=\angle CBE$。
$\because \angle F=\angle BCF$,$BF=BC$,$\therefore \triangle FBG\cong\triangle CBE$,$\therefore FG=CE$。
$\therefore EF=EG+FG=BE+CE=BE+AE$,即$BE + AE=EF$。故②正确。
如图②,连接$AC$交$BD$于点$O$,则$\angle DAO=\angle ACB=45^{\circ}$,过点$A$,$B$分别作$FC$的垂线,垂足分别为$K$,$N$。
$\because AB=1$,$\therefore$易得$AO=BO=\frac{\sqrt{2}}{2}AB=\frac{\sqrt{2}}{2}$,$AC=\sqrt{2}AB=\sqrt{2}$。
$\because \angle DAE=75^{\circ}$,$\angle DAO=45^{\circ}$,$\therefore \angle EAO=30^{\circ}$。
$\because$在正方形$ABCD$中,$AC\perp BD$,$\therefore EO=AO·\tan\angle EAO=\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{3}=\frac{\sqrt{6}}{6}$,$\therefore BE=OB - OE=\frac{\sqrt{2}}{2}-\frac{\sqrt{6}}{6}$。
$\because \angle BCE=15^{\circ}$,$\angle ACB=45^{\circ}$,$\therefore \angle ACK=30^{\circ}$,$\therefore AK=\frac{1}{2}AC=\frac{\sqrt{2}}{2}$。
在$Rt\triangle BEN$中,$BN=BE·\sin\angle NEB=BE·\sin60^{\circ}=(\frac{\sqrt{2}}{2}-\frac{\sqrt{6}}{6})×\frac{\sqrt{3}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$。
$\because AK\perp FC$,$BN\perp FC$,$\therefore KA// BN$,$\therefore \triangle AHK\sim\triangle BHN$,$\therefore \frac{AH}{BH}=\frac{AK}{BN}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}-\sqrt{2}}{4}}=\sqrt{3}+1$。故③错误。
$\because AB=AH + BH=1$,$\frac{AH}{BH}=\sqrt{3}+1$,$\therefore (\sqrt{3}+1)· BH + BH=1$,即$BH=\frac{1}{\sqrt{3}+2}=2-\sqrt{3}$。
如图③,$\because M$是边$BC$上一动点,将$\triangle BHM$沿$HM$翻折,点$B$落在点$P$处,$\therefore PQ\perp HM$,$\therefore \angle HQB=90^{\circ}$,$\therefore$点$Q$在以$HB$为直径的圆上运动。
取$HB$的中点$T$,连接$DT$,$\therefore$当点$Q$在$DT$上时,$DQ$的长取得最小值,最小值为$DT - BT$的值。
$\because BT=\frac{1}{2}BH=\frac{1}{2}(2 - \sqrt{3})=1-\frac{\sqrt{3}}{2}$,$\therefore AT=AB - BT=\frac{\sqrt{3}}{2}$。
$\therefore DT=\sqrt{AD^{2}+AT^{2}}=\sqrt{1+(\frac{\sqrt{3}}{2})^{2}}=\frac{\sqrt{7}}{2}$,$\therefore DT - BT=\frac{\sqrt{7}}{2}-(1-\frac{\sqrt{3}}{2})=\frac{\sqrt{7}+\sqrt{3}-2}{2}$。故④正确。
综上所述,正确的是①②④。



37. (2025·内蒙古)如图,ABCD是一张平行四边形纸片,BD是一条对角线,BD=BC=5,CD=6。
(1)如图①,将平行四边形纸片ABCD沿BD折叠,点A的对应点落在点P处,PB交CD于点M。
① 试猜想PM与CM的数量关系,并说明理由;
② 求△BDM的面积。
(2)如图②,点E,F分别在平行四边形纸片ABCD的边AB,AD上,连接EF,且EF // BD,将平行四边形纸片ABCD沿EF折叠,使点A的对应点G落在边CD上,求DG的长。

(1)如图①,将平行四边形纸片ABCD沿BD折叠,点A的对应点落在点P处,PB交CD于点M。
① 试猜想PM与CM的数量关系,并说明理由;
② 求△BDM的面积。
(2)如图②,点E,F分别在平行四边形纸片ABCD的边AB,AD上,连接EF,且EF // BD,将平行四边形纸片ABCD沿EF折叠,使点A的对应点G落在边CD上,求DG的长。

答案:
37.
(1)①$PM=CM$ 理由:由折叠,得$AD=DP$,$\angle DAB=\angle DPB$。
$\because$四边形$ABCD$是平行四边形,$\therefore AD=BC$,$\angle DAB=\angle BCD$,$\therefore DP=BC$,$\angle DPB=\angle BCD$。
又$\because \angle DMP=\angle BMC$,$\therefore \triangle DPM\cong\triangle BCM$,$\therefore PM=CM$。
②$\because \triangle DPM\cong\triangle BCM$,$\therefore DM=BM$。
如图①,过点$M$作$MN\perp BD$于点$N$,过点$B$作$BH\perp CD$于点$H$。
$\therefore DN=BN=\frac{1}{2}BD=\frac{5}{2}$。
$\because BD=BC=5$,$CD=6$,$\therefore DH=CH=\frac{1}{2}CD=3$。
$\therefore \cos\angle CDB=\frac{DH}{BD}=\frac{3}{5}=\frac{DN}{DM}=\frac{\frac{5}{2}}{DM}$,$\therefore DM=\frac{25}{6}$。
$\therefore MN=\sqrt{DM^{2}-DN^{2}}=\frac{10}{3}$,$\therefore S_{\triangle BDM}=\frac{1}{2}BD· MN=\frac{1}{2}×5×\frac{10}{3}=\frac{25}{3}$。
(2)如图②,过点$C$作$CP\perp BD$于点$P$,连接$AG$交$BD$于点$T$,过点$B$作$BH\perp CD$于点$H$。
由折叠,得$AG\perp EF$,$\because EF// BD$,$\therefore AG\perp BD$。
由
(1)②,可得$DH=CH=\frac{1}{2}CD=3$,$\therefore BH=\sqrt{BD^{2}-DH^{2}}=4$。
$\because S_{\triangle BCD}=\frac{1}{2}CD· BH=\frac{1}{2}BD· CP$,$\therefore CP=\frac{CD· BH}{BD}=\frac{24}{5}$。
$\therefore BP=\sqrt{BC^{2}-CP^{2}}=\frac{7}{5}$,$\therefore DP=BD - BP=5-\frac{7}{5}=\frac{18}{5}$。
$\because$四边形$ABCD$是平行四边形,$\therefore AD=BC$,$AD// CB$,$\therefore \angle ADT=\angle CBP$。
又$\because \angle ATD=\angle CPB=90^{\circ}$,$\therefore \triangle ADT\sim\triangle CBP$,$\therefore \frac{DG}{DC}=\frac{DT}{DP}=\frac{\frac{7}{5}}{\frac{18}{5}}$,解得$DG=\frac{7}{3}$。

37.
(1)①$PM=CM$ 理由:由折叠,得$AD=DP$,$\angle DAB=\angle DPB$。
$\because$四边形$ABCD$是平行四边形,$\therefore AD=BC$,$\angle DAB=\angle BCD$,$\therefore DP=BC$,$\angle DPB=\angle BCD$。
又$\because \angle DMP=\angle BMC$,$\therefore \triangle DPM\cong\triangle BCM$,$\therefore PM=CM$。
②$\because \triangle DPM\cong\triangle BCM$,$\therefore DM=BM$。
如图①,过点$M$作$MN\perp BD$于点$N$,过点$B$作$BH\perp CD$于点$H$。
$\therefore DN=BN=\frac{1}{2}BD=\frac{5}{2}$。
$\because BD=BC=5$,$CD=6$,$\therefore DH=CH=\frac{1}{2}CD=3$。
$\therefore \cos\angle CDB=\frac{DH}{BD}=\frac{3}{5}=\frac{DN}{DM}=\frac{\frac{5}{2}}{DM}$,$\therefore DM=\frac{25}{6}$。
$\therefore MN=\sqrt{DM^{2}-DN^{2}}=\frac{10}{3}$,$\therefore S_{\triangle BDM}=\frac{1}{2}BD· MN=\frac{1}{2}×5×\frac{10}{3}=\frac{25}{3}$。
(2)如图②,过点$C$作$CP\perp BD$于点$P$,连接$AG$交$BD$于点$T$,过点$B$作$BH\perp CD$于点$H$。
由折叠,得$AG\perp EF$,$\because EF// BD$,$\therefore AG\perp BD$。
由
(1)②,可得$DH=CH=\frac{1}{2}CD=3$,$\therefore BH=\sqrt{BD^{2}-DH^{2}}=4$。
$\because S_{\triangle BCD}=\frac{1}{2}CD· BH=\frac{1}{2}BD· CP$,$\therefore CP=\frac{CD· BH}{BD}=\frac{24}{5}$。
$\therefore BP=\sqrt{BC^{2}-CP^{2}}=\frac{7}{5}$,$\therefore DP=BD - BP=5-\frac{7}{5}=\frac{18}{5}$。
$\because$四边形$ABCD$是平行四边形,$\therefore AD=BC$,$AD// CB$,$\therefore \angle ADT=\angle CBP$。
又$\because \angle ATD=\angle CPB=90^{\circ}$,$\therefore \triangle ADT\sim\triangle CBP$,$\therefore \frac{DG}{DC}=\frac{DT}{DP}=\frac{\frac{7}{5}}{\frac{18}{5}}$,解得$DG=\frac{7}{3}$。

38. (2025·山东)【图形感知】
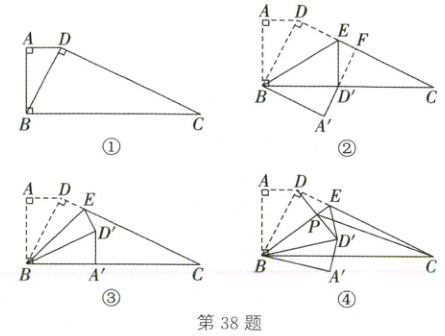
如图①,在四边形ABCD中,∠BAD=∠ABC=∠BDC=90°,AD=2,AB=4。
(1)求CD的长。
【探究发现】
老师指导同学们对如图①所示的纸片进行了折叠探究。
在线段CD上取一点E,连接BE。将四边形ABED沿BE翻折得到四边形A'BED',其中A',D'分别是点A,D的对应点。
(2)其中甲、乙两名同学的折叠情况如下:
① 甲:如图②,点D'恰好落在边BC上,延长A'D'交CD于点F,判断四边形DBA'F的形状,并说明理由;
② 乙:如图③,点A'恰好落在边BC上,求DE的长。
(3)如图④,连接DD'交BE于点P,连接CP。当点E在线段CD上运动时,线段CP的长是否存在最小值?若存在,求该最小值;若不存在,请说明理由。
如图①,在四边形ABCD中,∠BAD=∠ABC=∠BDC=90°,AD=2,AB=4。
(1)求CD的长。
【探究发现】
老师指导同学们对如图①所示的纸片进行了折叠探究。
在线段CD上取一点E,连接BE。将四边形ABED沿BE翻折得到四边形A'BED',其中A',D'分别是点A,D的对应点。
(2)其中甲、乙两名同学的折叠情况如下:
① 甲:如图②,点D'恰好落在边BC上,延长A'D'交CD于点F,判断四边形DBA'F的形状,并说明理由;
② 乙:如图③,点A'恰好落在边BC上,求DE的长。
(3)如图④,连接DD'交BE于点P,连接CP。当点E在线段CD上运动时,线段CP的长是否存在最小值?若存在,求该最小值;若不存在,请说明理由。

答案:
38.
(1)$\because \angle BAD=\angle ABC=\angle BDC=90^{\circ}$,$\therefore \angle BAD+\angle ABC=180^{\circ}$,$\therefore AD// BC$,$\therefore \angle ADB=\angle DBC$,$\therefore \triangle ADB\sim\triangle DBC$,$\therefore \frac{AD}{DB}=\frac{AB}{DC}$。
$\because \angle BAD=90^{\circ}$,$AD=2$,$AB=4$,$\therefore BD=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$,$\therefore \frac{2}{2\sqrt{5}}=\frac{4}{CD}$,$\therefore CD=4\sqrt{5}$。
(2)①四边形$DBA^{\prime}F$是矩形 理由:由折叠的性质,得$\angle A=\angle A^{\prime}=90^{\circ}$,$\angle ABD=\angle A^{\prime}BD^{\prime}$。
$\because \angle ABD+\angle DBC=\angle ABC=90^{\circ}$,$\therefore \angle A^{\prime}BD=\angle A^{\prime}BD^{\prime}+\angle DBC=90^{\circ}$,$\therefore \angle A^{\prime}BD=\angle BDC=\angle A^{\prime}=90^{\circ}$,$\therefore$四边形$DBA^{\prime}F$是矩形。
②如图①,延长$AD$和$A^{\prime}D^{\prime}$相交于点$Q$,连接$BQ$。
由折叠的性质,得$\angle A=\angle BA^{\prime}Q=90^{\circ}$,$\angle ABE=\angle A^{\prime}BE$,$AB=A^{\prime}B$。
$\because$点$A^{\prime}$恰好落在边$BC$上,$\therefore \angle ABA^{\prime}=90^{\circ}$,$\therefore$易得四边形$ABA^{\prime}Q$是矩形。
$\because AB=A^{\prime}B$,$\therefore$四边形$ABA^{\prime}Q$是正方形,$\therefore AQ=AB=4$,$AQ// CB$,$\therefore DQ=AQ - AD=4 - 2=2$。
在$Rt\triangle BCD$中,$BC=\sqrt{BD^{2}+CD^{2}}=\sqrt{(2\sqrt{5})^{2}+(4\sqrt{5})^{2}}=10$。
$\because \angle ABE=\angle A^{\prime}BE=\frac{1}{2}\angle ABA^{\prime}=45^{\circ}$,$\therefore$点$E$在对角线$BQ$上。
又$\because AQ// CB$,$\therefore \triangle DQE\sim\triangle CBE$,$\therefore \frac{DE}{CE}=\frac{DQ}{CB}=\frac{2}{10}=\frac{1}{5}$,$\therefore DE=\frac{1}{6}CD=\frac{2\sqrt{5}}{3}$。
(3)存在 由折叠的性质,得$BE$是线段$DD^{\prime}$的垂直平分线,$\therefore \angle BPD=90^{\circ}$,$\therefore$点$P$在以$BD$为直径的圆上。
如图②,取$BD$的中点$O$,连接$OC$,$OP$。
$\because CP\geqslant OC - OP$,$\therefore$当点$P$在$OC$上时,线段$CP$的长取得最小值。
$\because OP=OD=\frac{1}{2}BD=\sqrt{5}$,$\therefore OC=\sqrt{OD^{2}+CD^{2}}=\sqrt{(\sqrt{5})^{2}+(4\sqrt{5})^{2}}=\sqrt{85}$,$\therefore$线段$CP$的长的最小值为$OC - OP=\sqrt{85}-\sqrt{5}$。

38.
(1)$\because \angle BAD=\angle ABC=\angle BDC=90^{\circ}$,$\therefore \angle BAD+\angle ABC=180^{\circ}$,$\therefore AD// BC$,$\therefore \angle ADB=\angle DBC$,$\therefore \triangle ADB\sim\triangle DBC$,$\therefore \frac{AD}{DB}=\frac{AB}{DC}$。
$\because \angle BAD=90^{\circ}$,$AD=2$,$AB=4$,$\therefore BD=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$,$\therefore \frac{2}{2\sqrt{5}}=\frac{4}{CD}$,$\therefore CD=4\sqrt{5}$。
(2)①四边形$DBA^{\prime}F$是矩形 理由:由折叠的性质,得$\angle A=\angle A^{\prime}=90^{\circ}$,$\angle ABD=\angle A^{\prime}BD^{\prime}$。
$\because \angle ABD+\angle DBC=\angle ABC=90^{\circ}$,$\therefore \angle A^{\prime}BD=\angle A^{\prime}BD^{\prime}+\angle DBC=90^{\circ}$,$\therefore \angle A^{\prime}BD=\angle BDC=\angle A^{\prime}=90^{\circ}$,$\therefore$四边形$DBA^{\prime}F$是矩形。
②如图①,延长$AD$和$A^{\prime}D^{\prime}$相交于点$Q$,连接$BQ$。
由折叠的性质,得$\angle A=\angle BA^{\prime}Q=90^{\circ}$,$\angle ABE=\angle A^{\prime}BE$,$AB=A^{\prime}B$。
$\because$点$A^{\prime}$恰好落在边$BC$上,$\therefore \angle ABA^{\prime}=90^{\circ}$,$\therefore$易得四边形$ABA^{\prime}Q$是矩形。
$\because AB=A^{\prime}B$,$\therefore$四边形$ABA^{\prime}Q$是正方形,$\therefore AQ=AB=4$,$AQ// CB$,$\therefore DQ=AQ - AD=4 - 2=2$。
在$Rt\triangle BCD$中,$BC=\sqrt{BD^{2}+CD^{2}}=\sqrt{(2\sqrt{5})^{2}+(4\sqrt{5})^{2}}=10$。
$\because \angle ABE=\angle A^{\prime}BE=\frac{1}{2}\angle ABA^{\prime}=45^{\circ}$,$\therefore$点$E$在对角线$BQ$上。
又$\because AQ// CB$,$\therefore \triangle DQE\sim\triangle CBE$,$\therefore \frac{DE}{CE}=\frac{DQ}{CB}=\frac{2}{10}=\frac{1}{5}$,$\therefore DE=\frac{1}{6}CD=\frac{2\sqrt{5}}{3}$。
(3)存在 由折叠的性质,得$BE$是线段$DD^{\prime}$的垂直平分线,$\therefore \angle BPD=90^{\circ}$,$\therefore$点$P$在以$BD$为直径的圆上。
如图②,取$BD$的中点$O$,连接$OC$,$OP$。
$\because CP\geqslant OC - OP$,$\therefore$当点$P$在$OC$上时,线段$CP$的长取得最小值。
$\because OP=OD=\frac{1}{2}BD=\sqrt{5}$,$\therefore OC=\sqrt{OD^{2}+CD^{2}}=\sqrt{(\sqrt{5})^{2}+(4\sqrt{5})^{2}}=\sqrt{85}$,$\therefore$线段$CP$的长的最小值为$OC - OP=\sqrt{85}-\sqrt{5}$。

查看更多完整答案,请扫码查看


