《2025年金版新学案高中数学必修1人教版》

对点练 2. 已知奇函数$f(x)$的定义域为$[-5,5]$，且在区间$[0,5]$上的图象如图所示.

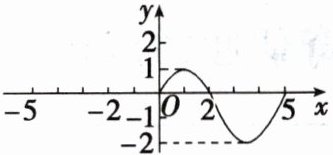
(1)补全函数$f(x)$的图象；
(2)写出使$f(x)＜0$的$x$的取值集合；
(3)写出函数$f(x)$的最值.

答案：
解:
(1)函数$f(x)$的图象如图所示。
(2)由图象可得使$f(x)＜0$的$x$的取值集合为$\{x\mid -2＜x＜0,或 2＜x＜5\}$。
　　　　　　　　　　　　　　　　　　　
(3)由图象可知$f(x)$的最大值为$2$，最小值为$-2$。

典例3 (1)若函数$f(x)=x^{2}+ax + 1$是定义在$(-b,2b - 2)$上的偶函数，则$f(\frac{b}{2})=$(D)

A.$\frac{1}{4}$
B.$\frac{5}{4}$
C.$\frac{7}{4}$
D.$2$

答案：
(1)D　
(1)根据题意，函数$f(x)=x^{2}+ax+1$ 是定义在$(-b,2b - 2)$上的偶函数，所以$\begin{cases}-b + 2b - 2 = 0\\a = 0\end{cases}$，则$\begin{cases}a = 0\\b = 2\end{cases}$。
　所以$f(x)=x^{2}+1$，则$f\left(\dfrac{b}{2}\right)=f(1)=1^{2}+1=2$。故选D。

(2)设$f(x)$是定义在$\mathbf{R}$上的奇函数，且当$x\geq0$时，$f(x)=x^{2}-\frac{1}{2}x$，则$f(-1)=$-\dfrac{1}{2}.

答案：
(2)$-\dfrac{1}{2}$　
(2)因为$f(x)$是定义在$\mathbf{R}$上的奇函数，所以$f(-1)=-f(1)=-\dfrac{1}{2}$。

(3)已知函数$f(x)=x^{7}-ax^{5}+bx^{3}+cx + 2$，若$f(-3)= -3$，则$f(3)=$7.
听课笔记：

答案：
(3)$7$　
(3)令$g(x)=x^{7}-ax^{5}+bx^{3}+cx$，则$g(x)$是奇函数，所以$f(-3)=g(-3)+2=-g(3)+2$，又$f(-3)=-3$，所以$g(3)=5$。又$f(3)=g(3)+2$，所以$f(3)=5 + 2 = 7$。

对点练 3. (1)设函数$f(x)=\frac{x^{2}+(a + 1)x + a}{x}$为奇函数，则实数$a$等于(A)

A.$-1$
B.$1$
C.$0$
D.$-2$

答案：
(1)A　
(1)法一:根据题意，知函数$f(x)=\dfrac{x^{2}+(a + 1)x + a}{x}$为奇函数，则有$f(x)+f(-x)=0$，即$\dfrac{x^{2}+(a + 1)x + a}{x}+\dfrac{x^{2}-(a + 1)x + a}{-x}=0$，变形可得$(a + 1)x = 0$，则有$a=-1$。故选A。
　法二:因为$f(x)=\dfrac{x^{2}+(a + 1)x + a}{x}$是奇函数，且$y = x$是奇函数，所以$y = x^{2}+(a + 1)x + a$是偶函数，则$a + 1 = 0$，故$a=-1$。故选A。

(2)已知$f(x)$是定义在$\mathbf{R}$上的奇函数，当$x＞0$时，$f(x)=x^{2}+mx + 1$，若$f(2)=3f(-1)$，则$m =$-\dfrac{11}{5}.

答案：
(2)$-\dfrac{11}{5}$　
(2)因为$x＞0$时，$f(x)=x^{2}+mx + 1$，所以$f(2)=5 + 2m$，$f(1)=2 + m$，又$f(-1)=-f(1)=-2 - m$，所以$5 + 2m = 3(-2 - m)$，解得$m=-\dfrac{11}{5}$。

1. 函数$y = f(x)$是奇函数，图象上有一点为$(a,f(a))$，则图象必过点 (C)

A.$(a,f(-a))$
B.$(-a,f(a))$
C.$(-a,-f(a))$
D.$(a,\frac{1}{f(a)})$

答案： 1.C

2. (多选)下列函数中，是奇函数的有 (BC)

A.$f(x)=x^{2}-2x + 2$
B.$f(x)=x^{3}+2x$
C.$f(x)=x-\frac{4}{x}$
D.$f(x)=|x|+\frac{1}{x^{2}}$

答案： 2.BC

3. 如图，给出奇函数$y = f(x)$的局部图象，则$f(-2)+f(-1)$的值为-2.

答案： 3.$-2$

4. 已知函数$f(x)=\begin{cases}x^{2}+x,x\leq0,\\ax^{2}+bx,x＞0\end{cases}$为奇函数，则$a - b =$ ______ .

答案： 4.$-2$