《2025年同步练习册山东科学技术出版社七年级数学上册鲁教版五四制》

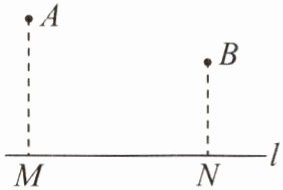
14. (12 分)如图,在平直的河岸 $ l $ 的同侧有 $ A $,$ B $ 两个村庄,$ A $,$ B $ 到 $ l $ 的距离 $ AM $,$ BN $ 分别是 $ 5 km $,$ 3 km $,且 $ MN = 6 km $。现计划在河岸上建一座抽水站 $ P $,用输水管向两个村庄 $ A $,$ B $ 供水,则输水管长度最少为多少？

答案：
解：如图，延长$AM$到点$A'$，使$MA'=MA$，连接$A'B$交$l$于点$P$，过$A'$作$A'C\perp BN$，交$BN$的延长线于点$C$。

因为$AM\perp l$，
所以$PA=PA'$。
由题意知四边形$MA'CN$是长方形，
所以$CN=MA'=5\ km$，$A'C=MN=6\ km$，
所以$BC=3+5=8\ km$。
在$Rt\triangle A'CB$中，由勾股定理得
$A'C^{2}+BC^{2}=A'B^{2}$，
所以$A'B=10\ km$。
所以$AP+BP=A'P+PB=A'B=10\ km$。
答：输水管长度最少为$10\ km$。

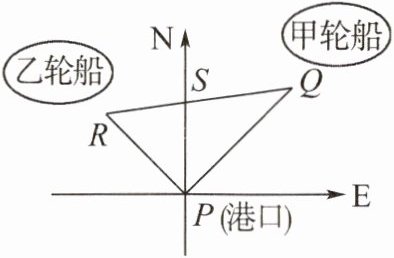
15. (12 分)某港口位于东西方向的海岸线上,甲、乙两艘轮船同时离开港口,各自沿固定方向航行,甲每小时航行 $ 16 n mile $,乙每小时航行 $ 12 n mile $,它们离开港口 $ 1.5 h $ 后相距 $ 30 n mile $。如图,如果知道甲轮船沿东北方向航行,那么能知道乙轮船沿哪个方向航行吗？

答案： 解：根据题意得
$PQ=16×1.5=24(n mile)$，
$PR=12×1.5=18(n mile)$，
$QR=30\ n mile$。
因为$24^{2}+18^{2}=30^{2}$，所以$PQ^{2}+PR^{2}=QR^{2}$，
所以$\angle QPR=90^{\circ}$。
由甲轮船沿东北方向航行可知$\angle QPS=45^{\circ}$，
则$\angle SPR=45^{\circ}$，
故乙轮船沿西北方向航行。

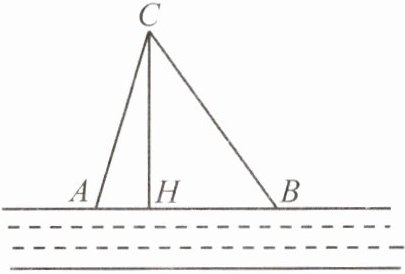
16. (14 分)如图,在一条东西走向的河的一侧有一个村庄 $ C $,河边原有两个取水点 $ A $,$ B $,其中 $ AB = AC $。由于某种原因,由 $ C $ 到 $ A $ 的路现在已经不通。为方便村民取水,决定在河边新建一个取水点 $ H $($ A $,$ H $,$ B $ 在一条直线上),并新修一条路 $ CH $,测得 $ CB = 3 km $,$ CH = 2.4 km $,$ BH = 1.8 km $。
(1)$ CH $ 是否为从村庄 $ C $ 到河边最近的路(即 $ CH $ 与 $ AB $ 是否垂直)？请通过计算加以说明。
(2)求原来的路线 $ AC $ 的长。

答案： 解：
(1)是。理由如下：
在$\triangle CHB$中，因为$CH=2.4\ km$，$BH=1.8\ km$，
所以$CH^{2}+BH^{2}=2.4^{2}+1.8^{2}=9$。
又因为$BC^{2}=9$，
所以$CH^{2}+BH^{2}=BC^{2}$，
所以$CH\perp AB$，
所以$CH$是从村庄$C$到河边最近的路。
(2)设$AC=x\ km$。
在$Rt\triangle ACH$中，由已知得
$AC=x\ km$，$AH=(x-1.8)\ km$，$CH=2.4\ km$。
由勾股定理得$AC^{2}=AH^{2}+CH^{2}$，
所以$x^{2}=(x-1.8)^{2}+2.4^{2}$，解得$x=2.5$。
答：原来的路线$AC$的长为$2.5\ km$。