《2025年同步练习册山东科学技术出版社七年级数学上册鲁教版五四制》

8. 如图,已知点 $A$,$D$,$C$,$F$ 在同一条直线上,$AB = DE$,$\angle ABC = \angle DEF$。给出下列三个条件：① $AC = DF$,② $BC = EF$,③ $\angle BAC = \angle EDF$。
(1)请在上述三个条件中选取一个,使得 $\triangle ABC \cong \triangle DEF$。你选取的条件序号为②,判定 $\triangle ABC \cong \triangle DEF$ 的依据是______SAS(填“$SSS$”或“$SAS$”或“$ASA$”或“$AAS$”)；
(2)请用(1)中所选的条件证明 $\triangle ABC \cong \triangle DEF$。

答案： 解:
(1)因为AB=DE,∠ABC=∠DEF,
所以当 BC=EF 时,利用"SAS"可以证明
△ABC≌△DEF;
当∠BAC=∠EDF时,利用"ASA"可以证明
△ABC≌△DEF。
(2)答案不唯一,例如选择②。
在△ABC和△DEF中,
AB=DE,
∠ABC=∠DEF,
BC=EF,
所以△ABC≌△DEF(SAS)。

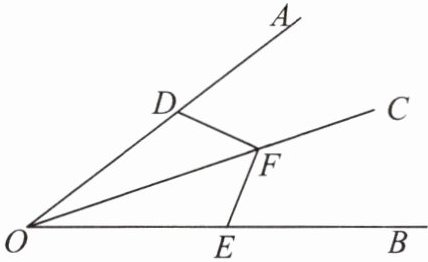
9. 如图,已知 $OC$ 是 $\angle AOB$ 的平分线,点 $D$ 在射线 $OA$ 上,点 $E$ 在射线 $OB$ 上,点 $F$ 在射线 $OC$ 上,连接 $DF$,$EF$。请添加一个条件,使 $\triangle OFD \cong \triangle OFE$。
小明同学写出以下条件：① $OD = OE$,② $\angle ODF = \angle OEF$,③ $\angle OFD = \angle OFE$,④ $FD = FE$,⑤ $\angle ADF = \angle BEF$,⑥ $\angle DFC = \angle EFC$。他认为添加以上条件中的任何一个,都可以使 $\triangle OFD \cong \triangle OFE$。
(1)小明的说法______(填“正确”或“错误”)；
(2)可以从小明写出的条件中选择______(填写序号),使得 $\triangle OFD \cong \triangle OFE$,并写出证明过程。

(1)小明的说法错误(填“正确”或“错误”)；
(2)可以从小明写出的条件中选择②(填写序号),使得 $\triangle OFD \cong \triangle OFE$,并写出证明过程。
证明：因为OC是∠AOB的平分线，所以∠DOF=∠EOF。在△OFD和△OFE中，∠DOF=∠EOF，∠ODF=∠OEF，OF=OF，所以△OFD≌△OFE(AAS)。

答案： 解:
(1)因为OC是∠AOB的平分线,
所以∠AOC=∠BOC。
①当OD=OE时,
由SAS可判定△OFD≌△OFE;
②当∠ODF=∠OEF时,
由AAS可判定△OFD≌△OFE;
③当∠OFD=∠OFE时,
由ASA可判定△OFD≌△OFE;
④当FD=FE时,∠AOC和∠BOC的对边分别
是FD和FE,不能判定△OFD≌△OFE;
⑤由∠ADF=∠BEF,可得到∠ODF=∠OEF,
由AAS可判定△OFD≌△OFE;
⑥由∠DFC=∠EFC,可得到∠OFD=∠OFE,
由ASA可判定△OFD≌△OFE。
所以小明的说法是错误的。
(2)选择②,证明如下:
因为OC是∠AOB的平分线,
所以∠DOF=∠EOF。
在△OFD和△OFE中,
∠DOF=∠EOF,
∠ODF=∠OEF,
OF=OF,
所以△OFD≌△OFE(AAS)。

10. 如图,在 $\triangle ABC$ 中,$AB = AC = 12\ cm$,$BC = 9\ cm$,点 $D$ 为 $AB$ 的中点。
(1)点 $P$ 在线段 $BC$ 上以 $3\ cm/s$ 的速度由点 $B$ 向点 $C$ 运动,同时点 $Q$ 在线段 $CA$ 上由点 $C$ 向点 $A$ 运动。
①若点 $Q$ 的运动速度与点 $P$ 的运动速度相等,则 $1\ s$ 时,$\triangle BPD$ 与 $\triangle CQP$ 是否全等？请说明理由。
②若点 $Q$ 的运动速度与点 $P$ 的运动速度不相等,则当点 $Q$ 的运动速度为多少时,能够使 $\triangle BPD \cong \triangle CPQ$？
(2)若点 $Q$ 以②中的运动速度从点 $C$ 出发,点 $P$ 以原来的速度从点 $B$ 同时出发,都逆时针沿 $\triangle ABC$ 的三边运动,则经过多长时间点 $P$ 与点 $Q$ 第一次在 $\triangle ABC$ 的哪条边上相遇？

答案： 解:
(1)①当t=1s时,
BP=CQ=3cm。
因为AB=12cm,点D为AB的中点,
所以BD=6cm。
又因为PC=BC-BP=9cm-3cm=6cm,
所以PC=BD。
因为AB=AC,
所以∠B=∠C。
在△BPD与△CQP中,
BP=CQ,
∠B=∠C,
BD=PC,
所以△BPD≌△CQP(SAS)。
②当△BPD≌△CQP时,
BP=CP=4.5cm,BD=CQ=6cm。
所以点P的运动时间t=4.5/3=1.5(s),
此时v_Q=CQ/t=6/1.5=4(cm/s)。
(2)因为v_Q＞v_P,所以只能是点Q追上点P,即
点Q比点P多走AB+AC的路程。
设经过x s点P与点Q第一次相遇,
依题意得4x=3x+2×12,
解得x=24,
此时点P运动了24×3=72(cm)。
又因为△ABC的周长为33cm,72=33×2+6,
所以点P,Q在BC边上相遇,即经过24s,点P
与点Q第一次在BC边上相遇。