《2025年同步练习册山东科学技术出版社七年级数学上册鲁教版五四制》

7. 底边长为 $ 10 cm $、底边上的高为 $ 12 cm $ 的等腰三角形的腰长为(B)
A.$ 12 cm $
B.$ 13 cm $
C.$ 8 cm $
D.$ 9 cm $

答案： B

8. 已知 $ a $,$ b $,$ c $ 是三角形的三边长,如果 $ a $,$ b $,$ c $ 满足 $ (a - 6)^{2} + (b - 8)^{2} + |c - 10| = 0 $,那么此三角形的形状是(D)
A.等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形

答案： D

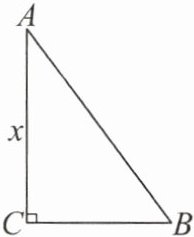
9. 《九章算术》是我国古代重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题：“今有竹高一丈,末折抵地,去本三尺,问折者高几何？”翻译成数学问题是：如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ AC + AB = 10 $,$ BC = 3 $,求 $ AC $ 的长。如果设 $ AC = x $,则可列方程$x^{2}+3^{2}=(10-x)^{2}$。

答案： $x^{2}+3^{2}=(10-x)^{2}$

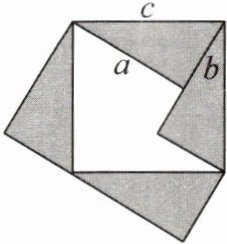
10. 小明将 4 个全等的直角三角形拼成如图所示的五边形,添加适当的辅助线后,用等面积法建立等式证明勾股定理。小明在证明过程中用两种方法表示出了五边形的面积,这两种方法求出的面积分别为 $ S_{1} = $$c^{2}+ab$,$ S_{2} = $$a^{2}+b^{2}+ab$。

答案： $c^{2}+ab$ $a^{2}+b^{2}+ab$（答案不唯一）

11. 我国南宋著名数学家秦九韶的著作《数书九章》中记载有这样一道题：“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何？”这道题讲的是：有一块三角形沙田,三边长分别为 5 里、12 里、13 里,问这块沙田面积有多大？题中的“里”是我国市制长度单位,$ 1 $ 里 $ = 0.5 km $,则该沙田的面积为7.5 $ km^{2} $。

答案： 7.5

12. 已知一个三角形的三边之比为 $ 5 : 12 : 13 $,周长为 60,则它的面积是120。

答案： 120

13. (10 分)为整治城市道路汽车超速现象,交警大队在某道路旁进行流动测速。如图,一辆小汽车在该城市道路上由东向西直行,某一时刻刚好行驶到车速检测仪 $ A $ 正北方向 $ 60 m $ 的 $ C $ 处,过了 $ 4 s $ 后,小汽车到达离车速检测仪 $ A $ $ 100 m $ 的 $ B $ 处。已知该段城市道路限速 $ 60 km/h $,则这辆小汽车是否超速？

答案： 解：超速。理由如下：
在$Rt\triangle ABC$中，$\angle C=90^{\circ}$，$AC=60\ m$，$AB=100\ m$，
由勾股定理得
$BC^{2}=AB^{2}-AC^{2}=100^{2}-60^{2}=80^{2}$，
所以$BC=80\ m$，
所以速度为$80\ m÷4\ s=20\ m/s=72\ km/h$。
因为$72＞60$，
所以这辆小汽车超速了。