《2025年同步练习册山东科学技术出版社七年级数学上册鲁教版五四制》

3. 小颖现有存款 $ 200 $ 元,她计划今后每月存款 $ 10 $ 元,则存款总金额 $ y $(单位：元)与时间 $ x $(单位：月)之间的函数表达式是(D)
A.$ y = 10x $
B.$ y = 120x $
C.$ y = 200 - 10x $
D.$ y = 200 + 10x $

答案： D

4. 李老师带领 $ x $ 名学生到动物园参观,已知成人票每张 $ 20 $ 元,学生票每张 $ 10 $ 元。设门票的总费用为 $ y $ 元,则 $ y = $10x+20。

答案： 10x+20

5. 用一根长为 $ 20 \, cm $ 的铁丝围成一个长方形,若该长方形的一边长为 $ x \, cm $,面积为 $ y \, cm^{2} $,则 $ y $ 与 $ x $ 之间的表达式为y=-x²+10x。

答案： y=-x²+10x

6. 同一温度的华氏度数 $ y $(单位：$ ^{\circ}F $)与摄氏度数 $ x $(单位：$ ^{\circ}C $)之间的函数表达式是 $ y = \frac{9}{5}x + 32 $。若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为-40$ ^{\circ}C $。

答案： -40

7. 甲、乙两地打电话需付的电话费 $ y $(单位：元)随通话时间 $ t $(单位：$ min $)的变化而变化,其关系如下表：

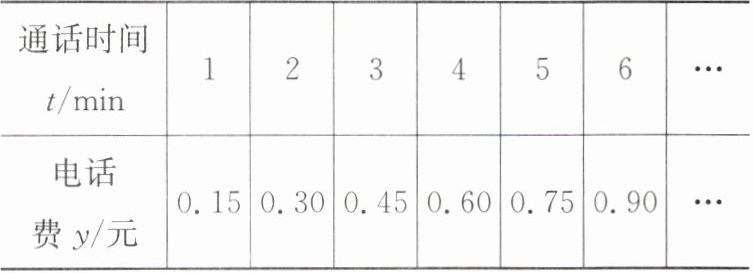
(1)自变量是通话时间,因变量是电话费；
(2)写出电话费 $ y $ 与通话时间 $ t $ 之间的表达式；
(3)若小明通话 $ 10 \, min $,则需付电话费多少元？
(4)若小明某次通话后付电话费 $ 4.8 $ 元,则小明通话多少分钟？
(2)y=0.15t
(3)当t=10时，y=0.15t=0.15×10=1.5。所以小明通话10min需付电话费1.5元。
(4)把y=4.8代入y=0.15t,得4.8=0.15t，解得t=32。所以当付电话费4.8元时,小明通话32min。

答案： 解:
(1)通话时间 电话费
(2)y=0.15t
(3)当t=10时，y=0.15t=0.15×10=1.5。所以小明通话10min需付电话费1.5元。
(4)把y=4.8代入y=0.15t,得4.8=0.15t，解得t=32。所以当付电话费4.8元时,小明通话32min。

8. 下列式子中,$ y $ 不是 $ x $ 的函数的是(B)
A.$ y = x^{2} $
B.$ |y| = x $
C.$ y = \frac{1}{x} $
D.$ y = 2x + 1 $

答案： B

9. 如图,下列各三角形中的三个数之间均具有相同的规律。根据此规律,最后一个三角形中 $ y $ 与 $ n $ 之间的关系是(C)

A.$ y = 2n + 1 $
B.$ y = 2^{n + 1} + n $
C.$ y = 2^{n} + n $
D.$ y = 2^{n} + n + 1 $

答案： C

10. 已知圆柱的高是 $ 5 \, cm $,圆柱的体积随圆柱底面半径的变化而变化。
(1)在这个变化过程中,自变量是圆柱的底面半径,因变量是圆柱的体积；
(2)如果圆柱的底面半径为 $ r $(单位：$ cm $),那么圆柱的体积 $ V $(单位：$ cm^{3} $)可以表示为$ V=5\pi r^{2} $；
(3)当 $ r $ 由 $ 1 \, cm $ 变化到 $ 10 \, cm $ 时,$ V $ 由$ 5\pi $$ cm^{3} $ 变化到$ 500\pi $$ cm^{3} $。

答案： 解:
(1)圆柱的底面半径 圆柱的体积
(2)V=5πr²
(3)5π 500π