《2025年同步练习册山东科学技术出版社七年级数学上册鲁教版五四制》

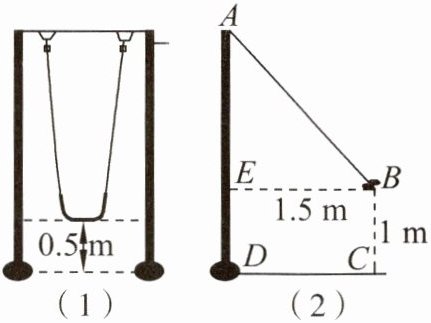
7. 如图是一副秋千架,图(1)是从正面看,当秋千绳子自然下垂时,踏板离地面$0.5m$(踏板厚度忽略不计)；图(2)是从侧面看,当秋千踏板荡起至点$B$位置时,点$B离地面的垂直高度BC为1m$,离秋千支柱$AD的水平距离BE为1.5m$(不考虑支柱的直径)。求秋千支柱$AD$的高。

[img]

答案： 解:设AD=xm,
　则AB=(x−0.5)m,AE=(x−1)m。
　在Rt△ABE中,AE²+BE²=AB²,
　即(x−1)²+1.5²=(x−0.5)²,
　解得x=3,
　故秋千支柱AD的高为3m。

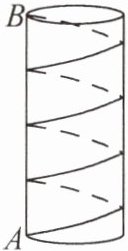
8. 如图,为了庆祝国庆节,学校准备在教学楼大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为$1m$,高为$3m$。如果要求彩带从柱子底端的$A处均匀地绕柱子4圈后到达柱子的顶端B$处(线段$AB$与地面垂直),那么彩带的长度至少为多少？

[img]

答案：
解:如图，把圆柱的侧面展开，得到四个长方形，其中AD,GE,HF,IJ,BC为圆柱的底面周长，
AB,CD为圆柱的高，
　　　　　　　　
　则AG=3÷4=0.75(m),
　所以GD²=AD²+AG²=1²+0.75²=1.25²,
　故GD=1.25m。
　4×1.25m=5m,所以彩带的长度至少为5m。

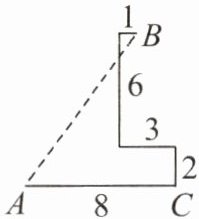
9. 假期中,小明和同伴到某海岛参加“探宝”游戏。按照如图所示的“探宝图”,他们从$A点登陆后先往东走8km$,又往北走$2km$,遇到障碍后又往西走了$3km$,再折向北走到$6km$处往东一拐,仅走了$1km$就找到了“宝藏”。问登陆点$A$到“宝藏”埋藏点$B$的直线距离是多少千米？

[img]

答案：
解:如图，过点B作BD⊥AC于点D。
　　　　　　　　
　根据题意可知AD=8−3+1=6(km),
　BD=2+6=8(km)。
　在Rt△ABD中,AB²=AD²+BD²=6²+8²=10²,所以AB=10km。
　答:登陆点A到“宝藏”埋藏点B的直线距离为10km。