第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
7. 有两把不同的锁和两把不同的钥匙,其中每一把钥匙都只能打开其中的一把锁,打不开另一把锁。现在任意取出一把钥匙去开任意一把锁,则一次打开锁的概率为
$\frac{1}{2}$
。
答案:
$\frac{1}{2}$
8. 有四张背面完全相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图3-1-2-3),将这四张纸牌背面朝上洗匀。
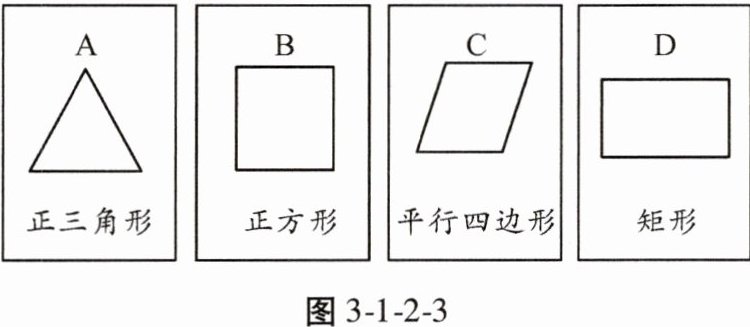
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形,则小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或画树状图法)说明理由。

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形,则小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或画树状图法)说明理由。
答案:
解:
(1)因为共有4张牌,牌面图形是中心对称图形的情况有3种,所以摸出的牌面图形是中心对称图形的概率是$\frac{3}{4}$。
(2)这个游戏公平。理由:列表如下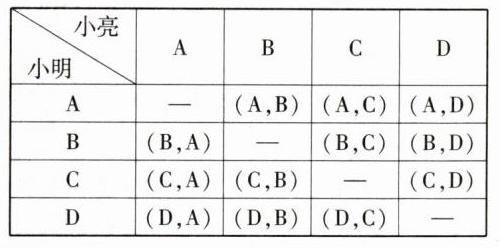
∵共有12种结果,每种结果出现的可能性相同,其中两张牌面图形都是轴对称图形的有6种,
∴P(两张牌面图形都是轴对称图形)=$\frac{1}{2}$,因此这个游戏公平。
解:
(1)因为共有4张牌,牌面图形是中心对称图形的情况有3种,所以摸出的牌面图形是中心对称图形的概率是$\frac{3}{4}$。
(2)这个游戏公平。理由:列表如下

∵共有12种结果,每种结果出现的可能性相同,其中两张牌面图形都是轴对称图形的有6种,
∴P(两张牌面图形都是轴对称图形)=$\frac{1}{2}$,因此这个游戏公平。
9. “手心、手背”是在同学中广为流传的游戏。游戏时,甲、乙、丙三方每次出“手心”“手背”两种手势中的一种,规定:①出现三个相同的手势不分胜负,继续比赛;②出现一个“手心”和两个“手背”或者出现一个“手背”和两个“手心”时,则出一种手势者为胜,两种相同手势者为负。
(1)假定甲、乙、丙三人每次都是等可能地出“手心”或“手背”,请用画树状图或列表的方法求甲、乙、丙三位同学获胜的概率;
(2)若甲同学只出“手背”,乙、丙两位同学仍随机地出“手心”或“手背”,则甲同学获胜的可能性会减小吗?为什么?
(1)假定甲、乙、丙三人每次都是等可能地出“手心”或“手背”,请用画树状图或列表的方法求甲、乙、丙三位同学获胜的概率;
(2)若甲同学只出“手背”,乙、丙两位同学仍随机地出“手心”或“手背”,则甲同学获胜的可能性会减小吗?为什么?
答案:
解:
(1)画树状图如下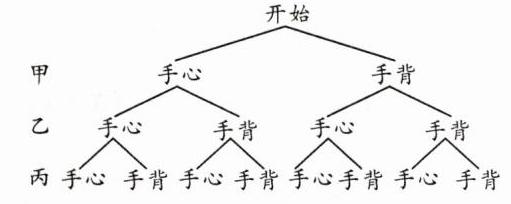
∵一共有8种结果,每种结果出现的可能性相等,其中甲、乙、丙三位同学获胜的结果各有2种,
∴P(甲获胜)=P(乙获胜)=P(丙获胜)=$\frac{2}{8}=\frac{1}{4}$。
(2)甲同学获胜的可能性不会减小。理由:画树状图如下 一共有4种结果,每种结果出现的可能性相等,其中甲获胜的结果有1种,
一共有4种结果,每种结果出现的可能性相等,其中甲获胜的结果有1种,
∴甲获胜的概率仍为$\frac{1}{4}$,可能性不会减小。
解:
(1)画树状图如下

∵一共有8种结果,每种结果出现的可能性相等,其中甲、乙、丙三位同学获胜的结果各有2种,
∴P(甲获胜)=P(乙获胜)=P(丙获胜)=$\frac{2}{8}=\frac{1}{4}$。
(2)甲同学获胜的可能性不会减小。理由:画树状图如下
 一共有4种结果,每种结果出现的可能性相等,其中甲获胜的结果有1种,
一共有4种结果,每种结果出现的可能性相等,其中甲获胜的结果有1种,∴甲获胜的概率仍为$\frac{1}{4}$,可能性不会减小。
查看更多完整答案,请扫码查看


