第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
【例 1】如图 4 - 6 - 1,身高为 1.65 m 的小明想测量学校旗杆的高度,当他站在 C 处时,他影子的顶端正好与旗杆影子的顶端重合,并测得 AC = 3 m,BC = 6 m,则旗杆的高度为
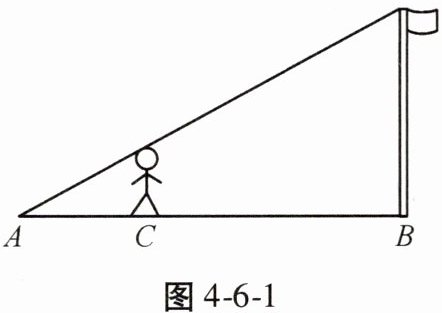
解题关键 将实物图形转化为相似模型解答。
4.95
m。
解题关键 将实物图形转化为相似模型解答。
答案:
4.95
【例 2】如图 4 - 6 - 2,在一次数学活动课上,小芳到操场上测量旗杆的高度,她的测量方法是:拿一根长 3.5 m 的竹竿直立在离旗杆 27 m 的 C 处,然后沿 BC 方向走到 D 处,这时

目测旗杆顶部 A 与竹竿顶部 E 恰好在同一直线上,又测得 C,D 两点的距离为 3 m。已知小芳的目高为 1.5 m,利用她所测得的数据,求旗杆的高度。
解题关键 根据已知过点 F 作 FG ⊥ AB,垂足为 G,交 CE 于点 H,利用相似三角形的判定得出△AGF ∽ △EHF,即可求解。

目测旗杆顶部 A 与竹竿顶部 E 恰好在同一直线上,又测得 C,D 两点的距离为 3 m。已知小芳的目高为 1.5 m,利用她所测得的数据,求旗杆的高度。
解题关键 根据已知过点 F 作 FG ⊥ AB,垂足为 G,交 CE 于点 H,利用相似三角形的判定得出△AGF ∽ △EHF,即可求解。
答案:
解:如图,过点F作FG⊥AB,垂足为G,交EC于点H。
根据题意可得∠AGF=∠EHF=90°,EC=3.5m,BC=GH=27m,CD=FH=3m,
DF=CH=BG=1.5m,
则EH=EC - CH=2m,GF=GH+HF=30m。

又
∵∠EFH=∠AFG,
∴△AGF∽△EHF,
∴$\frac{AG}{EH}=\frac{GF}{FH}$,即$\frac{AG}{2}=\frac{30}{3}$,解得AG=20。
∴AB=AG+BG=20+1.5=21.5(m)。
因此旗杆的高度为21.5m。
解:如图,过点F作FG⊥AB,垂足为G,交EC于点H。
根据题意可得∠AGF=∠EHF=90°,EC=3.5m,BC=GH=27m,CD=FH=3m,
DF=CH=BG=1.5m,
则EH=EC - CH=2m,GF=GH+HF=30m。

又
∵∠EFH=∠AFG,
∴△AGF∽△EHF,
∴$\frac{AG}{EH}=\frac{GF}{FH}$,即$\frac{AG}{2}=\frac{30}{3}$,解得AG=20。
∴AB=AG+BG=20+1.5=21.5(m)。
因此旗杆的高度为21.5m。
查看更多完整答案,请扫码查看


