《2025年绩优学案九年级数学上册北师大版》

1. 黄金分割数$\frac{\sqrt{5}-1}{2}$是一个很奇妙的数,它被大量应用于艺术、建筑和统计决策等方面。请你估算$\sqrt{5}-1$的值(B)
A.在1.1和1.2之间
B.在1.2和1.3之间
C.在1.3和1.4之间
D.在1.4和1.5之间

答案： B

2. 已知点P为线段AB的黄金分割点,且$AP ＜ PB$,则下列各式正确的是(C)
A.$AP^{2}= AB\cdot PB$
B.$AB^{2}= AP\cdot PB$
C.$PB^{2}= AP\cdot AB$
D.$PA^{2}= AP\cdot BP$

答案： C

3. 美是一种感觉,当人体下半身的长度与身高的比值越接近0.618时,越给人一种美感。张女士的身高为168cm,下半身长为1.02m,为了达到更好的美感,她应该选择4.8cm的高跟鞋。(结果精确到0.1cm)

答案： 4.8

4. 如图4-4-4-3,点C和D均为线段AB的黄金分割点,$CD = 6$,求AB的长。

答案： $AB=6\sqrt{5}+12$

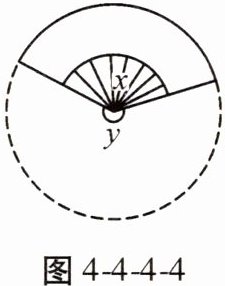
5. 如图4-4-4-4,扇子的圆心角的度数为x,余下扇形的圆心角的度数为y,x与y的比通常按黄金比来设计,这样的扇子外形较美观,若取黄金比为0.6,则x为(B)

A.$216^{\circ}$
B.$135^{\circ}$
C.$120^{\circ}$
D.$108^{\circ}$

答案： B

6. 英才学校数学兴趣小组举行了趣味数学活动,小刚用学过的黄金分割知识设计了一幅作品,作品的宽与长的比为黄金比,已知作品的其中一边长为20cm,则它的另一边长为$10(\sqrt{5}-1)cm$或$10(\sqrt{5}+1)cm$。(结果保留根号)

答案： $10(\sqrt{5}-1)cm$或$10(\sqrt{5}+1)cm$

7. 如图4-4-4-5,在$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,$\angle 1 = \angle 2$,点D是线段AC的黄金分割点吗？说明理由。

答案： 解:D是AC的黄金分割点。理由:$\because$在$\triangle ABC$中,$AB=AC$,$\angle A=36°$,$\therefore \angle ABC=\angle ACB=72°$。$\because \angle 1=\angle 2$,$\therefore \angle 1=\angle 2=\frac{1}{2}\angle ABC=36°$。$\therefore$在$\triangle BDC$中,$\angle BDC=180° -\angle 2-\angle C=72°$,$\therefore \angle C=\angle BDC$,$\therefore BC=BD$。$\because \angle A=\angle 1$,$\therefore AD=BC$。$\because$在$\triangle ABC$和$\triangle BDC$中,$\angle 2=\angle A$,$\angle C=\angle C$,$\therefore \triangle ABC\backsim \triangle BDC$,$\therefore \frac{AB}{BD}=\frac{BC}{CD}$。又$\because AB=AC$,$AD=BC=BD$,$\therefore \frac{AC}{AD}=\frac{AD}{CD}$,$\therefore AD^2=AC\cdot CD$,即D是AC的黄金分割点。