《2025年绩优学案九年级数学上册北师大版》

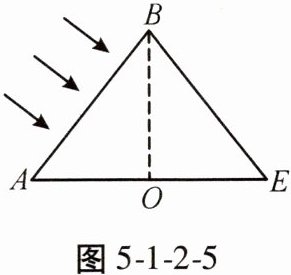
8. 如图5-1-2-5,阳光照射在一棵因暴雨发生地陷而倾斜的电线杆AB上。已知AB的长为6 m,此时B点到地面的距离为3 m,某时刻身高为1.8 m的小明在太阳光下的影子长为2.4 m,求此时电线杆的影长AE。

答案： 解:
∵AB=6m,BO=3m,由勾股定理得AO²+BO²=AB²,
∴AO=√(AB² - BO²)=3√3m。设OE的长为xm,则3/x = 1.8/2.4,解得x=4,
∴AE=AO+OE=(3√3+4)m。

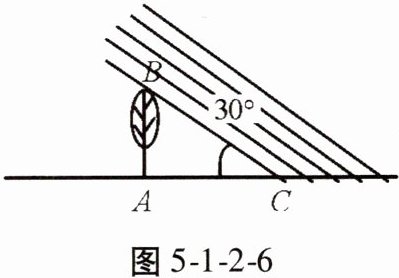
9. 某数学兴趣小组利用树影测量树高。如图5-1-2-6,已测出树AB的影长AC为12 m,并测出此时太阳光线与地面成30°夹角。
(1)求树高AB；
(2)因水土流失,此时树AB沿光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,求树的最大影长。

答案： 解:
(1)4√3m　
(2)当树与地面成60°角时影长最长(或树与光线垂直时影长最长),AC=2AB=8√3m。

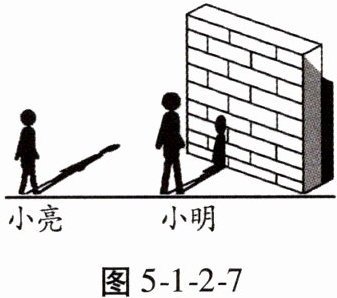
10. 如图5-1-2-7,小明和小亮在阳光下玩耍,小亮对小明说：“我的身高为1.6 m,你的身高我不知道,但我量出此时你、我的影长,我就能求出你的身高。”小明不服气,当他们走到了一堵墙前时,小明的影子没有全部落在地面上,有一部分落在墙上,小明灵机一动,问小亮：“现在你能求出我的身高吗?”小亮说：“那还不容易,我的影长(全在地面上)为2.4 m,你的影长 = 墙上的影长 + 地上的影长 = 0.6 + 1.8 = 2.4 (m),那么你的身高就是(1.6×2.4)/2.4 = 1.6 (m)。”小明哈哈大笑：“照你这么说,我与你一样高啦。”小明在小亮耳边说了几句话,小亮就恍然大悟。你知道小亮错在哪吗?

答案：
解:建立如图所示的示意图。 设AB为小亮，CD为小明,GF为小明在墙上的影子。
∵太阳光线是平行的，作直线AE//CG，过F作FH//CG,则CH=FG=0.6m,且△ABE∽△HDF,
∴AB/BE = DH/DF,即1.6/2.4 = DH/1.8,即DH=1.8×1.6÷2.4=1.2(m)。即小明的身高为1.2+0.6=1.8(m)。