《2025年绩优学案九年级数学上册北师大版》

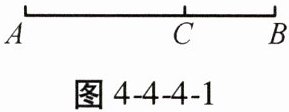
【例1】如图4-4-4-1,点C是线段AB的黄金分割点。
(1) 若$AC = 1$,求BC,AB的长；
(2) 若$BC = 1$,求AC,AB的长。

解题关键 根据黄金分割中的线段关系求值。

答案： 解:
(1)由题得$AC=\frac{\sqrt{5}-1}{2}AB$,$\because AC=1$,$\therefore AB=\frac{\sqrt{5}+1}{2}$,$\therefore BC=AB-AC=\frac{\sqrt{5}-1}{2}$。
(2)由题得$AC=\frac{\sqrt{5}-1}{2}AB$,$\therefore BC=AB-AC=\frac{3-\sqrt{5}}{2}AB$。$\because BC=1$,$\therefore AB=\frac{3+\sqrt{5}}{2}$,$\therefore AC=AB-BC=\frac{\sqrt{5}+1}{2}$。

【例2】如图4-4-4-2,电视节目的主持人在主持节目时,站在舞台的黄金分割点处最自然得体。若舞台AB长为20m,主持人现在站在A处,请问主持人应走到离A点多少米处才最自然得体？(结果精确到0.1m)

解题关键 依据黄金比的定义即可求解。

答案： 主持人应走到离A点约7.6m或12.4m处最自然得体。