第96页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
9.(2024·濮阳期中)如图,表格中是直角三角形的是( )
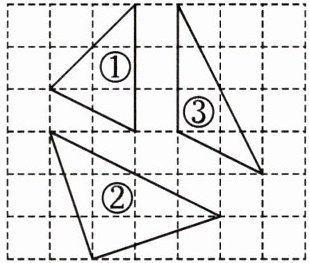
A.①
B.②
C.③
D.①②

A.①
B.②
C.③
D.①②
答案:
B
10.新考向 开放性问题 将勾股数3,4,5分别扩大为原来的2倍、3倍、4倍……可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数.请写出两组不同于以上所给出的基本勾股数:
答案不唯一,如:5,12,13;7,24,25
.
答案:
答案不唯一,如:5,12,13;7,24,25
11.(2024·南阳方城县期末)笔直的河流一侧有一旅游地点G,河边有两个漂流点A,B,且点A到点B的距离等于点A到点G的距离.近阶段由于点G到点A的路线处于维修中,为方便游客,决定在河边新建一个漂流点C(点A,B,C在同一条直线上),并新建一条路GC,测得BG=5km,GC=4km,BC=3km.
(1)判断△BCG的形状,并说明理由;
(2)求原路线GA的长.
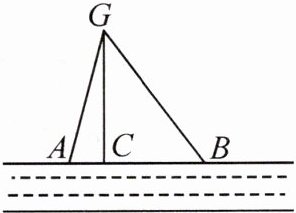
(1)判断△BCG的形状,并说明理由;
(2)求原路线GA的长.

答案:
解:
(1)△BCG是直角三角形.理由如下:
∵BG=5km,GC=4km,BC=3km,且4²+3²=5²,
∴GC²+BC²=BG².
∴△BCG是直角三角形.
(2)
∵点A到点B的距离等于点A到点G的距离,
∴AG=AB.
∵由
(1)可知,△ACG是直角三角形,
∴设AG=AB=xkm,则AC=(x-3)km.在Rt△ACG中,由勾股定理,得AC²+GC²=GA²,即(x-3)²+4²=x²,解得x=25/6.
∴原路线GA的长为25/6km.
(1)△BCG是直角三角形.理由如下:
∵BG=5km,GC=4km,BC=3km,且4²+3²=5²,
∴GC²+BC²=BG².
∴△BCG是直角三角形.
(2)
∵点A到点B的距离等于点A到点G的距离,
∴AG=AB.
∵由
(1)可知,△ACG是直角三角形,
∴设AG=AB=xkm,则AC=(x-3)km.在Rt△ACG中,由勾股定理,得AC²+GC²=GA²,即(x-3)²+4²=x²,解得x=25/6.
∴原路线GA的长为25/6km.
12.用反证法证明命题“若△ABC的三边长a,b,c(a≤b<c)满足a²+b²≠c²,则△ABC不是直角三角形”时,第一步应先假设
△ABC为直角三角形
.
答案:
△ABC为直角三角形
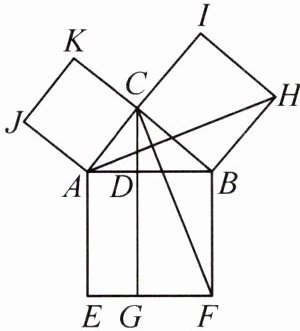
13.华师二附中校本经典题 已知:在Rt△ABC中,∠C=90°,AC=b,BC=a,AB=c.求证:a²+b²=c².
【背景文化】勾股定理是数学史上非常重要的一个定理,2000多年来,人们对它进行了大量的研究,它的证明方法多达300余种.
【证明思路】下面是《几何原本》中证明勾股定理的几个步骤:如图,分别以Rt△ABC的三边为边作正方形ABFE、正方形AJKC、正方形BCIH,过点C作AB的垂线,交AB于点D,交FE于点G,连结HA,CF.第一步可证明△ABH≌△FBC;第二步可证明正方形BCIH的面积与四边形BFGD的面积相等;第三步可证明a²+b²=c².
【问题解决】综合上述内容,完成以下证明.
(1)求证:△ABH≌△FBC;
(2)求证:正方形BCIH的面积与四边形BFGD的面积相等;
(3)求证:a²+b²=c².
【背景文化】勾股定理是数学史上非常重要的一个定理,2000多年来,人们对它进行了大量的研究,它的证明方法多达300余种.
【证明思路】下面是《几何原本》中证明勾股定理的几个步骤:如图,分别以Rt△ABC的三边为边作正方形ABFE、正方形AJKC、正方形BCIH,过点C作AB的垂线,交AB于点D,交FE于点G,连结HA,CF.第一步可证明△ABH≌△FBC;第二步可证明正方形BCIH的面积与四边形BFGD的面积相等;第三步可证明a²+b²=c².
【问题解决】综合上述内容,完成以下证明.
(1)求证:△ABH≌△FBC;
(2)求证:正方形BCIH的面积与四边形BFGD的面积相等;
(3)求证:a²+b²=c².

答案:
证明:
(1)
∵四边形ABFE和四边形CBHI都是正方形,
∴AB=FB,HB=CB,∠ABF=∠CBH=90°.
∴∠HBA=∠CBF.
∴△ABH≌△FBC(SAS).
(2)
∵∠ACB+∠BCI=90°+90°=180°,
∴A,C,I三点共线.
∴AI//BH.
∴S△ABH=1/2S正方形BCIH.
∵CG//BF,
∴S△FBC=1/2S长方形BFGD.又
∵△ABH≌△FBC,
∴S△ABH=S△FBC.
∴S正方形BCIH=S长方形BFGD,即正方形BCIH的面积与四边形BFGD的面积相等.
(3)同
(2)可得,正方形ACKJ的面积与四边形ADGE的面积相等.
∴S正方形ACKJ+S正方形BCIH=S长方形ADGE+S长方形BFGD=S正方形ABFE,即AC²+BC²=AB².
∴a²+b²=c².
(1)
∵四边形ABFE和四边形CBHI都是正方形,
∴AB=FB,HB=CB,∠ABF=∠CBH=90°.
∴∠HBA=∠CBF.
∴△ABH≌△FBC(SAS).
(2)
∵∠ACB+∠BCI=90°+90°=180°,
∴A,C,I三点共线.
∴AI//BH.
∴S△ABH=1/2S正方形BCIH.
∵CG//BF,
∴S△FBC=1/2S长方形BFGD.又
∵△ABH≌△FBC,
∴S△ABH=S△FBC.
∴S正方形BCIH=S长方形BFGD,即正方形BCIH的面积与四边形BFGD的面积相等.
(3)同
(2)可得,正方形ACKJ的面积与四边形ADGE的面积相等.
∴S正方形ACKJ+S正方形BCIH=S长方形ADGE+S长方形BFGD=S正方形ABFE,即AC²+BC²=AB².
∴a²+b²=c².
查看更多完整答案,请扫码查看


